Гидродинамика идеальной несжимаемой жидкости.
1. Идеальная жидкость. В тех случаях, когда роль сил трения в текущих жидкостях сравнительно невелика, ими можно пренебречь. Такая модель жидкости, в которой отсутствует трение, называется идеальной жидкостью. Законы динамики идеальной жидкости наиболее просты.
2. Линии тока. Для описания идеальной жидкости применяется понятие линий тока. Это линии, в каждой точке которых вектор скорости движения частиц жидкости направлен по касательной. По сути – это траектории движущихся частиц (рис.94).
Непрерывное множество линий тока образуют трубку тока (рис.95).
3. Уравнение неразрывности струи. Из условия постоянства объема жидкости следует уравнение неразрывности струи. В любой момент времени объемы жидкости, протекающие в трубке тока через сечения в разных ее частях, одинаковы. Отсюда v1s1 = v2s2 =¼= const. (29.1)
Это уравнение неразрывности. Здесь v – линейная скорость движения частиц жидкости.
4. Уравнение Бернулли. Если внешние силы, вызывающие движение жидкости, не зависят от времени, то через некоторое время после начала движения в жидкости установится вполне определенное распределение скоростей. Такое движение жидкости называется установившимся (стационарным).
В 1738 г. Даниило Бернулли вывел соотношение между величинами, характеризующими стационарное движение идеальной несжимаемой жидкости.
p+ 
+ rgh = const. Уравнение Бернулли (29.2)
|
|
|
Уравнение Бернулли выражает закон сохранения энергии применительно к идеальной жидкости. Здесь – кинетическая энергия единичного объема жидкости, rgh – потенциальная энергия единичного объема жидкости в поле силы тяжести, p - внутрижидкостное давление.
Размерности энергии (единицы объема) и давления совпадают. Поэтому члены уравнения Бернулли называют еще так: p - статический напор, rgh - гидравлический напор, - динамический напор. Если записать уравнение для двух сечений s1 и s2 , трубки тока (рис.96) p1+ 
+ rgh1 = p2+ 
+ rgh2, то легко видеть, что чем меньше сечение трубки s, тем больше скорость течения жидкости, тем больше динамический напор и тем меньше статический напор − давление на стенки.
| Даниило (Даниил) Бернулли (I700–I782) – математик и физик, представитель швейцарской династии Бернулли. Основная работа – “Гидродинамика” (I738). Наряду с Эйлером является создателем теоретической гидродинамики. |
5. Формула Торричелли. Воспользуемся уравнением Бернулли для определения скорости вытекания струи из узкого отверстия в стенке широкого сосуда (рис.97).
Пусть из сосуда с жидкостью, площадь зеркала которой s1, вытекает из отверстия в стенке, площадь которого s2 << s1 струя. Запишем уравнение Бернулли для сечений s1 и s2.
|
|
|
p1+ + rgh1 = p2+ + rgh2.
Статическое давление в жидкости в сечениях s1 и s2 одинаковое (атмосферное), поэтому p1 = p2.Начало координат выбрано так, чтобы h2 = 0. Отсюда
rgh1 = и v2 = 
. Формула Торричелли, 1641г. (29.3)
Идеальная жидкость вытекает из сосуда с высотой уровня над отверстием h с такой же скоростью, с какой она свободно падала бы с этой же высоты.
6. Течение жидкости в горизонтальной трубе переменного сечения. Выясним, как изменяется давление в разных точках трубы переменного сечения (рис.98). Так как h1 = h2 , то уравнение Бернулли для сечений s1 и s2 принимает вид: p1 + = p2 + . Из уравнения неразрывности v1s1 = v2s2. Тогда v2 = v1s1/s2, и перепад давления составляет p1 - p2 = 
. (29.4)
Чем меньше сечение трубы, тем больше скорость течения жидкости, тем меньше статический напор. В узких местах трубы статический напор может сделаться меньше, чем давление снаружи трубы. В этом случае, если в стенке трубы сделать отверстие, то труба будет действовать как насос. Так действуют, например, водоструйный насос, пульверизатор, карбюратор.
7. Обтекание несимметричных тел. Подъемная сила. Рассмотрим обтекание полуцилиндра. Поскольку жидкость несжимаема, то при обтекании полуцилиндра частицам жидкости, находящимся на линиях тока 1 и 2 , приходится проходить разный путь и, следовательно, двигаться с разными скоростями (рис.99).
|
|
|
Запишем уравнение Бернулли для линий тока 1 и 2: p1 + = p2+ . Здесь v1çv2 = pRç2R, откуда v1 = pv2ç2. Между нижней и верхней поверхностями полуцилиндра возникает перепад давлений
p2 - p1 = - = 
. (29.5)
На плоскую поверхность давление больше, чем на выпуклую. В результате перепада давлений возникает сила, которую называют подъемной (рис.100). F = DP×s (29.6)
В общем случае подъемная сила возникает всегда, когда обтекаемое жидкостью тело несимметрично. Эта сила в значительной мере делает возможным горизонтальный полет летательных машин тяжелее воздуха. Наряду с подъемной силой здесь используется также подъемная составляющая динамического напора, обусловленная положительным углом атаки крыла (рис.101).
§ 30. Гидродинамика вязкой несжимаемой жидкости
1. Вязкая жидкость. Закон Ньютона. Реальные жидкости в отличие от идеальной имеют вязкость, она проявляется в том, что при движении слоев жидкости параллельно друг другу между ними возникает сила трения (рис.102).
|
|
|
F = hs 
. 3акон Ньютона, 1687 (30.1)
Здесь s - площадь соприкасающихся слоев. Величина определяет скорость изменения скорости течения жидкости в направлении, перпендикулярном слоям жидкости, и называется градиентом скорости. Коэффициент h называют коэффициентом вязкости или динамической вязкостью жидкости. Это характеристика жидкости. Чем больше h, тем больше внутреннее трение, тем более вязкая жидкость.
Единица h в СИ – паскаль-секунда, 1 Па×с = 1 Н×с/м2.
С повышением температуры динамическая вязкость жидкостей уменьшается, газов – увеличивается. В таблице 30.1 приведены значения h некоторых жидкостей и газов.
| Таблица 30.1 | |||
| Вязкость жидкостей при 293 К | Вязкость газов при 293 К и pатм | ||
| Ацетон Вода Спирт этиловый Ртуть Глицерин | 0,32×10-3Па×с 1,00×10-3Па×с 1,20×10-3Па×с 1,55×10-3Па×с 1480×10-3Па×с | Азот Водород Воздух Углекислый газ Кислород | 1,75×10-5Па×с 0,88×10-5Па×с 1,82×10-5Па×с 1,47×10-5Па×с 2,02×10-5Па×с |
2. Вязкое течение. Формула Пуазейля. Движение жидкости, при котором ее слои скользят друг по другу без завихрений, а линии тока не имеют разрывов, называется вязким (ламинарным). В 1841г. французский врач Жан Пуазейль (I799–I869) экспериментально установил закон истечения вязкой жидкости через тонкую цилиндрическую трубу постоянного сечения: V= 
. Формула Пуазейля, 1841 (30.2)
Здесь V – объем жидкости, протекающей в единицу времени через сечение трубки радиусом R и длиной l, Dp – перепад давления на концах трубки.
Отношение 
есть градиент давления, то есть скорость изменения давления вдоль трубы (рис.103).
Падение внутрижидкостного давления в трубе объясняется диссипацией механической энергии текущей жидкости. Так как жидкость несжимаема, то динамический напор в трубе постоянного сечения не может уменьшаться, = const. Поэтому рассеивание механической энергии, то есть превращение ее в тепло, происходит за счет убыли статического напора.
Формула Пуазейля используется, например, в капиллярных вискозиметрах – приборах для измерения вязкости жидкостей и газов.
Скорость движения частиц идеальной жидкости во всех точках сечения прямолинейной трубы одинакова. А в вязкой жидкости скорость движения ее частиц убывает по мере удаления от оси трубы. Огибающая векторов скоростей частиц жидкости, медленно текущей по цилиндрической трубе, образует параболу. Говорят, вязкая жидкость в цилиндрической трубе имеет параболический профиль скоростей (рис.104).
3. Вязкое обтекание шара. Формула Стокса. В 1851г. английский физик Джордж Стокс (I8I9–I903) теоретически вывел формулу, определяющую силу действия на твердый шар со стороны медленно обтекающей его вязкой жидкости.
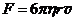. Формула Стокса, 1851 (30.3)
Здесь r - радиус шара, v - скорость движения частиц жидкости на бесконечном удалении от шара.
На использовании формулы Стокса основан один из методов определения вязкости жидкостей (рис.105).
В трубу большого диаметра, поставленную вертикально и заполненную исследуемой жидкостью, опускают маленький шарик из вещества, плотность которого больше плотности жидкости. Шарик тонет. Если радиус его не более 1–2 мм, то через 1–2 с он движется равномерно. В этом случае FA+Fh= mg, (30.4)
или 
. Þ 
. (30.5)
Здесь h = vt – отрезок, на котором шарик падает равномерно, t –время падения шарика на этом отрезке.
4. Турбулентное движение жидкости. Число Рейнольдса. Рассмотренные выше случаи справедливы лишь при малых скоростях движения жидкости, когда силы вязкого трения (это т.н. поверхностные силы) больше сил инерции (это массовые, или объемные силы).
С увеличением скорости роль сил инерции частиц жидкости увеличивается, слоистый характер течения жидкости нарушается, линии тока рвутся, появляются вихри. Ламинарное течение переходит в турбулентное. (Ламинарное – от латинского lamina – пластинка, турбулентное –от латинского turbulentus – бурный, беспорядочный).
В 1876–83г.г. английский инженер Осборн Рейнольдс (I842–I9I2) экспериментально нашел количественный критерий перехода ламинарного течения в цилиндрических трубах в турбулентное. Re = 
Число Рейнольдса (30.6)
Здесь r – плотность жидкости, v – средняя скорость ее течения в трубе, d – диаметр трубы. Число Рейнольдса есть отношение кинетической энергии единичного объема текущей жидкости к работе вязких сил в этом объеме.
При малой скорости, то есть при малом числе Re течение жидкости или газа будет ламинарным. Если скорость растет и достигает значения, соответствующего критическому значению числа Reкр, то ламинарное течение переходит в турбулентное.
Критерий Рейнольдса является универсальным, он применим не только к цилиндрическим трубам, но и к другим профилям каналов, а также к случаям обтекания жидкостью препятствий. Так, например, при обтекании шара Reкр@1, при течении жидкости в цилиндре Reкр@1000. Однако значения Reкр сильно зависят от состояния поверхностей тел. В общем случае d – характеристический размер. Применительно к шару d – это диаметр шара, применительно к препятствию произвольной формы – размер препятствия, применительно к каналу – ширина канала.
5. Метод подобия в гидромеханике. Число Рейнольдса является одним из критериев подобия в гидромеханике. Закон подобия гласит: два сравниваемых геометрически подобных потока подобны и гидромеханически, если равны соответствующие им числа Рейнольдса, то есть 
.
Этот закон дает возможность проводить экспериментальное исследование сложных процессов, используя малые модели обтекаемых тел. Например, обдувание в аэродинамических трубах моделей самолетов, моделей телевизионных вышек (под ветровые нагрузки), моделей автомобилей и т.д. Однако нельзя сделать модель как угодно малой (и тем самым удешевить испытания), поскольку с уменьшением размеров тел приходится увеличивать скорости потоков, чтобы Re оставалось постоянным. При скоростях потоков, близких к скорости звука в данной жидкости или газе эти среды уже нельзя считать несжимаемыми. Наряду с числом Рейнольдса в гидромеханике используются и другие критерии подобия.
Так, например, при скоростях, сравнимых со скоростью звука, используют число Маха М, равное отношению скорости движения тела v к скорости звука vзв, то есть M = v/vзв. В случае необходимости учета влияния сил тяжести используется число Фруда Fr = v2/gd, равное отношению инерционных сил к силам тяжести. Критерии подобия являются безразмерными числами. Методы подобия используются не только в гидромеханике, но и в теории упругости, теориях теплопроводности, диффузии, электромагнетизма и др.
Дата добавления: 2018-04-15; просмотров: 1412; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!