Гидростатика несжимаемой жидкости
1. Несжимаемые жидкости и газы. В отличие от твердых тел газы и жидкости не обладают постоянством формы. Они обладают лишь объемной упругостью. Сжимаемость жидкостей очень мала, и в подавляющем большинстве явлений жидкости можно считать практически несжимаемыми. Газы же сжимаются легче, и в большинстве явлений их сжимаемость проявляется отчетливо.
В настоящем разделе мы ограничимся таким кругом явлений, в которых эффекты сжимаемости настолько незначительны, что ими можно пренебречь.
2. Основные понятия.Основными величинами, определяющими состояние несжимаемой жидкости, являются давление p, плотность жидкости r и ее объем V.
Давление P определяется силой нормального напряжения, p =  . Единица давления в СИ - паскаль, 1 Па = 1 Н/м2. Кроме того, используются кратные единицы: гектопаскаль: 1 гПа = 100 Па, килопаскаль: 1 кПа = 1000 Па, и т.д. Плотность вещества r определяется отношением массы вещества к объему, который она занимает, r =
. Единица давления в СИ - паскаль, 1 Па = 1 Н/м2. Кроме того, используются кратные единицы: гектопаскаль: 1 гПа = 100 Па, килопаскаль: 1 кПа = 1000 Па, и т.д. Плотность вещества r определяется отношением массы вещества к объему, который она занимает, r =  .
.
Для измерения плотности жидкостей используются ареометры. Давление в жидкостях и газах измеряется манометрами.
3. Закон Паскаля. Жидкости и газы не имеют регулярной структуры в расположении атомов и молекул, их свойства одинаковы по всем направлениям. Говорят, жидкости и газы изотропны. (От греч. isos – равный и tropos – направление).
В 1663 году французский ученый Блез Паскаль открыл закон, вытекающий из свойства изотропности жидкостей:
|
|
|
Давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково по всем направлениям.
Этот закон справедлив также и для газов. Правда, у газов нет свободной поверхности, поэтому смысл закона Паскаля сводится к тому, что в небольших газовых объемах, находящихся в равновесии, давление во всех точках одинаково.
 4. Гидростатическое давление. Давление внутри жидкости на глубине h равно p = rgh (рис.87). Это так называемое гидростатическое давление. Действительно, p =
4. Гидростатическое давление. Давление внутри жидкости на глубине h равно p = rgh (рис.87). Это так называемое гидростатическое давление. Действительно, p =  . (28.1)
. (28.1)
С увеличением глубины давление увеличивается. Если учесть еще атмосферное давление, то p = p0 + rgh, (28.2)
где p0 – атмосферное давление на уровне поверхности жидкости.
 Гидростатическое давление не зависит от конфигурации сосудов, в которых находится жидкость. Давление есть функция только высоты (глубины). Поэтому сила давления на дно сосуда зависит только от высоты уровня жидкости и площади дна (рис.88). Этот факт называют иногда гидростатическим парадоксом. Из него же следует и закон сообщающихся сосудов.
Гидростатическое давление не зависит от конфигурации сосудов, в которых находится жидкость. Давление есть функция только высоты (глубины). Поэтому сила давления на дно сосуда зависит только от высоты уровня жидкости и площади дна (рис.88). Этот факт называют иногда гидростатическим парадоксом. Из него же следует и закон сообщающихся сосудов.
5. Закон Архимеда был открыт в 3-м веке до н.э. В современной формулировке он гласит:
На всякое тело, погруженное в жидкость, (или газ) действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной этим телом жидкости.
|
|
|
Сила Архимеда направлена вверх и приложена к геометрическому центру погруженной части тела (рис.89).
 Чтобы тело, погруженное в жидкость полностью или частично, находилось в равновесии, нужно, чтобы сумма сил, действующих на тело, была равной нулю.
Чтобы тело, погруженное в жидкость полностью или частично, находилось в равновесии, нужно, чтобы сумма сил, действующих на тело, была равной нулю.
 . (28.3)
. (28.3)
 Это условие плавания тел. В зависимости от формы плавающего тела и положения его центра тяжести равновесие может быть устойчивым, неустойчивым и безразличным (рис.90).
Это условие плавания тел. В зависимости от формы плавающего тела и положения его центра тяжести равновесие может быть устойчивым, неустойчивым и безразличным (рис.90).
Точка приложения равнодействующей сил Архимеда называется центром плавучести.

 Если центр плавуче-сти выше центра тяжести, то положение равновесия устойчивое, если ниже - неустойчивое. Если точки A и С совпадают, равновесие безразличное.
Если центр плавуче-сти выше центра тяжести, то положение равновесия устойчивое, если ниже - неустойчивое. Если точки A и С совпадают, равновесие безразличное.
6. Свободная поверхность жидкости в равновесии в поле консервативных сил совпадает с эквипотенциальной поверхностью (рис.91).
Касательная к поверхности жидкости в любой ее точке перпендикулярна вектору силы.
 Если жидкость находится в НИСО, то поверхность жидкости нормальна вектору силы суммарного силового поля.
Если жидкость находится в НИСО, то поверхность жидкости нормальна вектору силы суммарного силового поля. 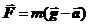 . (28.4)
. (28.4)
Так, если НИСО движется поступательно с ускорением  , то поверхность жидкости образует с вектором ускорения свободного падения угол a, причем tga=
, то поверхность жидкости образует с вектором ускорения свободного падения угол a, причем tga=  (рис.92).
(рис.92).
|
|
|
 Свободная поверхность во вращающемся сосуде принимает форму параболоида вращения (рис.93). Действительно, если ОУ – вертикальная ось, a r – полярный радиус, то из выражения тангенса угла между касательной к поверхности жидкости и горизонталью получаем дифференциальное уравнение линии, образуемой осевым сечением поверхности жидкости.
Свободная поверхность во вращающемся сосуде принимает форму параболоида вращения (рис.93). Действительно, если ОУ – вертикальная ось, a r – полярный радиус, то из выражения тангенса угла между касательной к поверхности жидкости и горизонталью получаем дифференциальное уравнение линии, образуемой осевым сечением поверхности жидкости.
 .
.
Постоянная С определяется объемом налитой в сосуд жидкости. Пример: ртутное зеркало телескопа Вуда.
Дата добавления: 2018-04-15; просмотров: 1610; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
