ГЛАВА 2. ДИНАМИКА ТВЕРДОГО ТЕЛА
Абсолютно твердое тело. Движение твердого тела
1. Твердое тело. Понятием "твердое тело" (ТТ) в физике обозначается одно из 4-х агрегатных состояний вещества, отличающееся от других агрегатных состояний – жидкости, газов и плазмы –стабильностью формы и характером теплового движения атомов. Для механики, рассматривающей движение ТТ в пространстве, наиболее существенным свойством ТТ является стабильность его формы.
Однако, у реальных твердых тел объём и форма могут изменяться в зависимости от физических воздействий. Поэтому уравнения движения твердого тела в механике получены применительно к идеализированной модели, называемой абсолютно твердым телом. Абсолютно твердое тело – это такое тело, у которого объём, форма и распределение плотностей остаются неизменными во времени независимо от действия внешних сил и скорости движения тела.
Такая модель АТТ применима лишь в классической механике при малых скоростях движения точек тела.
 2. Степени свободы ТТ. Связи. Положение твердого тела в пространстве определяется координатами любых 3-х точек, принадлежащих телу (рис.45).
2. Степени свободы ТТ. Связи. Положение твердого тела в пространстве определяется координатами любых 3-х точек, принадлежащих телу (рис.45).
Но поскольку это АТТ, то благодаря постоянству расстояний между точками число независимых координат уменьшается с 9 до 6. Говорят, ТТ имеет 6 степеней свободы: 3 степени свободы определяют поступательное движение ТТ, а 3 – его вращательное движение.
 Ограничения, налагаемые на движение тела другими телами, называются связями. Связи уменьшают число степеней свободы. Так, тело, посаженное на гладкую бесконечную ось ОХ, имеет только две степени свободы (рис.46). Одна – это линейная координата X, определяющая смещение тела вокруг оси ОХ, другая – угловая координата, определяющая угол поворота тела вокруг оси ОХ.
Ограничения, налагаемые на движение тела другими телами, называются связями. Связи уменьшают число степеней свободы. Так, тело, посаженное на гладкую бесконечную ось ОХ, имеет только две степени свободы (рис.46). Одна – это линейная координата X, определяющая смещение тела вокруг оси ОХ, другая – угловая координата, определяющая угол поворота тела вокруг оси ОХ.
|
|
|
 3. Поступательное движение ТТ. Любое сложное движение ТТ можно представить как сумму двух простых движений – поступательного и вращательного.
3. Поступательное движение ТТ. Любое сложное движение ТТ можно представить как сумму двух простых движений – поступательного и вращательного.
Поступательным движением ТТ называют такое его движение, при котором все точки тела описывают одинаковые траектории (рис.47). При поступательном движении ТТ его ориентация в пространстве остаётся неизменной, а все точки ТТ в любой момент времени имеют одинаковые скорости и ускорения. Число степеней свободы поступательного движения равно 3.
 4. Вращательное движение ТТ. Вращением ТТ вокруг неподвижной оси называется такое его движение, при котором траектории всех точек тела образуют множество окружностей с центром на одной прямой, называемой осью вращения. Ось вращения может лежать вне тела или проходить сквозь тело (рис.48).
4. Вращательное движение ТТ. Вращением ТТ вокруг неподвижной оси называется такое его движение, при котором траектории всех точек тела образуют множество окружностей с центром на одной прямой, называемой осью вращения. Ось вращения может лежать вне тела или проходить сквозь тело (рис.48).
Скорость движения точек тела при вращении его вокруг неподвижной оси есть  , (21.1)
, (21.1)
|
|
|
где w – угловая скорость вращения, а r – радиус-вектор, проведенный от оси вращения к точке.
 Когда траектории движения тела образуют множество плоских фигур, движение тела называют плоским или плоскопараллельным.
Когда траектории движения тела образуют множество плоских фигур, движение тела называют плоским или плоскопараллельным.
5. Сложное плоскопараллельное движение ТТ. В этом случае скорость движения произвольной точки тела есть сумма скоростей,  , (21.2)
, (21.2)
где v0 – скорость поступательного движения произвольно выбранного центра O (центра СК, связанной с ТТ), r – радиус-вектор, проведенный из точки O в ту точку тела, скорость которой определяется (рис.49).
Угловая скорость вращения ТТ не зависит от того, в какой точке ТТ она определяется, во всех точках ТТ она имеет одно значение.
Произвол в выборе центра O влияет лишь на величины v0 и r, но так, что скорость движения данной точки ТТ  целом не зависит от этого выбора. Поэтому центр O выбирают так, чтобы исследование движения тела было наиболее простым.
целом не зависит от этого выбора. Поэтому центр O выбирают так, чтобы исследование движения тела было наиболее простым.
6. Мгновенная ось вращения. При любом движении тела в каждое мгновение существует единственная неподвижная точка, которая может быть как внутри тела, так и вне его. Скорости движения всех точек ТТ в это мгновение распределены так, как они распределяются при вращении тела вокруг неподвижной оси.
|
|
|

 Такая неподвижная точка называется мгновенным центром вращения. В случае плоского движения множество мгновенных центров вращения образуют мгновенную ось вращения, перпендикулярную плоскости движения. В отличие от неподвижной оси, сохраняющей свое положение как в теле, так и в пространстве, мгновенная ось вращения в общем случае перемещается как в теле, так и в пространстве (рис.50).
Такая неподвижная точка называется мгновенным центром вращения. В случае плоского движения множество мгновенных центров вращения образуют мгновенную ось вращения, перпендикулярную плоскости движения. В отличие от неподвижной оси, сохраняющей свое положение как в теле, так и в пространстве, мгновенная ось вращения в общем случае перемещается как в теле, так и в пространстве (рис.50).

 Мгновенная ось вращения при плоском движении находится как точка пересечения перпендикуляров к векторам скоростей (рис.51). Если известны векторы скоростей двух точек ТТ v1 и v2, то можно найти не только мгновенную ось вращения ТТ, но и его угловую скорость вращения.
Мгновенная ось вращения при плоском движении находится как точка пересечения перпендикуляров к векторам скоростей (рис.51). Если известны векторы скоростей двух точек ТТ v1 и v2, то можно найти не только мгновенную ось вращения ТТ, но и его угловую скорость вращения.  . (21.3)
. (21.3)
7. Пара сил. Две силы, равные по величине, но противоположные по направлению, приложенные к двум разным точкам твердого тела, образуют пару сил. Вычислим её вращающий момент (рис.52).
Выберем на прямой, соединяющей точки 1 и 2, произвольный центр 0, от которого будем отсчитывать расстояния до точек приложения сил F1 и F2. Моменты сил относительно точки 0 есть  . (21.4)
. (21.4)
Результирующий момент равен их сумме,  . (21.5)
. (21.5)
Представим расстояние между точками 1 и 2 как вектор l, направленный из точки 2 в точку 1. Так как l = r1 - r2, а 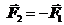 , то
, то  . (21.6)
. (21.6)
|
|
|
Вектор l называется плечом пары. Координаты точки O выпали из выражения момента пары. Следовательно, действие пары сил на ТТ не меняется, если пару сил переносить куда угодно в плоскости пары или в плоскости, ей параллельной. Момент пары сил можно считать приложенным к любой точке тела.
Пара сил не имеет равнодействующей, поэтому пару сил нельзя уравновесить одной силой. Моменты пар сил суммируются как векторы.
8. Динамика поступательного движения ТТ. Любое твердое тело можно интерпретировать как систему материальных точек. Поэтому движение ТТ может быть определено системой уравнений движения этих материальных точек.  . (21.7)
. (21.7)
При поступательном движении скорости и ускорения всех точек одинаковы, а внешние силы суммируются в равнодействующую. Чтобы тело двигалось без поворотов, нужно, чтобы равнодействующая сил была приложена к точке центра масс тела.
 Таким образом, уравнение поступательного движения твердого тела сводится к уравнению движения его центра масс.
Таким образом, уравнение поступательного движения твердого тела сводится к уравнению движения его центра масс.  . (21.7)
. (21.7)
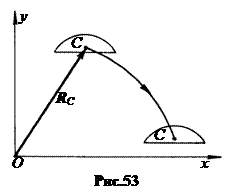
Здесь с – центр масс ТТ, RC – радиус-вектор, проведенный из начала системы координат в точку центра масс (рис.53).
Итак, при поступательном движении твердое тело может моделироваться материальной точкой, расположенной в центре масс ТТ и имеющей массу, равную массе тела.
Дата добавления: 2018-04-15; просмотров: 539; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
