Вращение ТТ вокруг неподвижной оси

1. Уравнение вращательного движения ТТ вокруг неподвижной оси. Будем рассматривать ТТ как систему материальных точек. В этом случае движение СМТ определится суммой уравнений движения всех точек тела (рис.54). . (22.1)

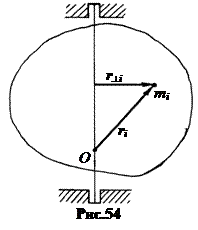Здесь a_i – ускорение, которое испытывает каждая материальная точка тела.

Все точки двигаются по окружностям, поэтому ускорение складывается из центростремительного a_^i и касательного , где e – угловое ускорение тела.

Отсюда 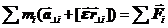.                        (22.2)

Умножим обе части равенства под знаком суммы векторно на радиус-вектор r_^i слева.

.              (22.3)

Но векторы r_^i и a_^i противоположны, следовательно,   Раскроем двойное векторное произведение:

. Но , кроме того,  – сумма моментов внешних сил. Итак, .                                   (22.4)

Назовём моментом инерции твердого тела (или системы материальных точек) относительно оси вращения величину =I .                                                (22.5)

Тогда 2-й закон динамики для вращательного движения ТТ вокруг неподвижной оси будет иметь вид: .                                                                                            (22.6)

Угловое ускорение, испытываемое твердым телом при вращении его вокруг оси, пропорционально моменту внешних сил относительно этой оси и обратно пропорционально моменту инерции тела относительно той же оси.

2. Осевой момент инерции ТТ зависит от распределения масс в теле и является мерой инертности тела при вращательном движении. Если при решении задач динамики поступательного движения достаточно знать массу тела и действующие на него силы, то при вращательном движении вокруг фиксированной оси нужно знать ещё и геометрию масс (распределение массы в пространстве), необходимую для вычисления момента инерции, и точки приложения внешних сил, чтобы найти их моменты относительно оси вращения.

Момент инерции сплошного твердого тела может быть вычислен суммированием моментов инерции его частей по формуле (22.5) или интегрированием: I = .  (22.7)

Так как dm =r(r)dV, где r – плотность, dV – элемент объема, то I = 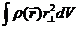.    (22.8)

Здесь r_^ – расстояние до оси вращения.

Пример 22.1 Момент инерции точки относительно оси I = m .            (22.9)

Пример 22.2 Момент инерции однородного стержня постоянного сечения относительно конца (т.е. относительно оси перпендикулярной стержню и проходящей через его конец). Длина стержня L, линейная плотность его (т.е. масса, приходящаяся на единицу его длины,) – g = m/L = const (рис.55).

Так как dm = gdr  есть масса элемента стержня, длиной dr, то формула (22.7) принимает вид:

.              (22.10)

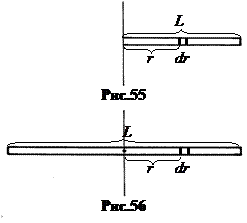
Пример 22.3 Момент инерции однородного стержня относительно оси, проходящей через его середину (рис.56), можно найти с помощью предыдущей формулы путем несложных рассуждений:

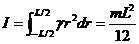.                                (22.11)

Пример 22.4 Момент инерции сплошного цилиндрического диска относительно геометрической оси(рис.57). В полярных координатах dV=2prbdr. Отсюда  или . Но 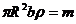 – масса диска. Тогда .     (22.12)

Пример 22.5 Момент инерции толстого кольца относительно геометрической оси (т.е. диска радиуса , из которого вынут коаксиальный диск радиуса ) (рис.58). Очевидно, из момента инерции сплошного диска нужно вычесть момент инерции отсутствующей части диска. Тогда .                                            (22.13)

Запишем еще несколько формул без вывода.

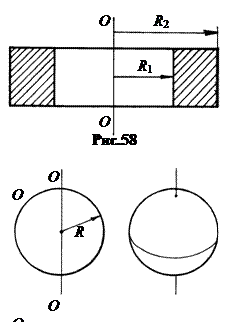Пример 22.6 Момент инерции бесконечно тонкого диска относительно диаметра (рис.59).   /                                          (22.14)

Пример 22.7 Момент инерции сплошного однородного шара относительно диаметра (рис.60).   

/                                                (22.15)

3. Задача. Определить ускорение движения грузов m₁ и m₂, подвешенных на невесомой нити, перекинутой через цилиндрический блок массой m₃ (рис.61).

Система состоит из трех тел – двух грузов и массивного блока. Грузы m₁ и m₂ двигаются поступательно, поэтому могут моделироваться материальными точками. Блок вращается вокруг неподвижной оси. Составляем систему 3-х уравнений:      (22.16)

Здесь I – момент инерции блока (сплошного диска) по формуле (22.12).

Для решения системы уравнения нужно спроектировать на оси. Движение грузов m₁ и m₂ в данной задаче проектируем на вертикальную ось ОХ. Третье уравнение проектируем на ось вращения блока, на ось OZ. Поскольку движения всех трех тел согласованы между собой, то и направление оси вращения должно быть согласовано с направлением траектории движения грузов m₁ и m₂ по правилу правого винта.

Записываем уравнения в проекции.

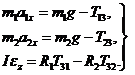                                              (22.17)

Доопределим систему c семью неизвестными недостающими четырьмя уравнениями – «уравнениями связи». Нить нерастяжимая, значит a_1x = −a_2x . Нить невесомая, значит . Кроме того, R₁ = R₂ = R, а произведение  Ie_z преобразуем, подставив  и

. Итак:

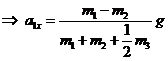. (22.18)

---

Дата добавления: 2018-04-15; просмотров: 535; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!