Момент импульса и момент силы. Законы сохранения
1. Момент импульса. Воспользуемся векторным способом описания движения материальной точки. Во многих случаях, когда точка движется под действием силы по криволинейной траектории, этот способ исследования движения плодотворнее координатного. Особенно, если траекторией является кривая 2-го порядка (окружность, эллипс, парабола, гипербола). При этом не только упрощается исследование, но и открываются качественно новые свойства материи.
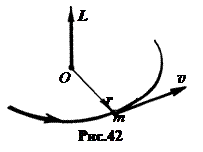Моментом импульса L материальной точки относи-тельно полюса O (рис.42) называется векторное произведение радиуса-вектора r на импульс точки p: 
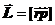. (20.1)
Векторное произведение векторов a и b есть вектор 
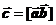, который направлен в сторону поступательного дви-жения правого винта, если вращать его по кратчайшему пути от первого сомножителя (вектора a) ко второму (вектору b). Длина вектора c равна произведению длин перемножаемых векторов на синус угла между ними, c = absin(a^b).
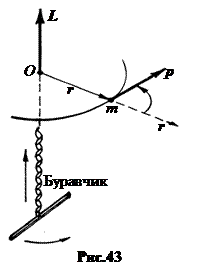
Очевидно, вектор момента импульса L перпендикулярен плоскости, в которой лежат перемножаемые векторы r и p (рис.43). Длина вектора L равна L = rpsin(r^p).
Если определяется момент импульса относительно некоторой оси, проходящей через полюс O, то вектор L в этом случае просто проектируется на эту ось. Здесь Ly = Lcos(L^j) − момент импульса относительно оси OY.
2.Уравнение моментов. Продифференцируем вектор момента импульса L по времени t: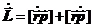 
. (20.2)
По 2-му закону динамики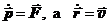 
– скорость движения материальной точки. Векторное произведение двух коллинеарных векторов 
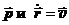равно нулю (синус угла между ними равен нулю). Отсюда 
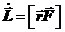. Векторное произведение 
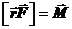называют моментом силы F относительно полюса 0. Получаем:
|
|
|
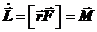. Уравнение моментов (20.3)
Скорость изменения момента импульса материальной точки относительно некоторого центра O равна моменту действующей силы относительно того же центра.
3. Момент импульса точки в поле центральных сил. Если на материальную точку m действует центральная сила, направленная вдоль paдиуса-вектора r (рис.44), то векторы r и F направлены вдоль одной прямой, а их векторное произведение равно нулю,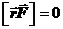 
. Следовательно, момент центральной силы равен нулю. Если точка m движется только под действием центральных сил, то уравнение моментов принимает вид: 
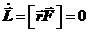Þ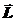 
= const. (20.4)
Момент импульса материальной точки в поле центральных сил есть величина постоянная.
Это значит, что вектор L имеет постоянные длину и направление, а траектория движения точки есть кривая, лежащая в плоскости, перпендикулярной вектору L.
4. Момент импульса СМТ. Моментом импульса системы материальных точек относительно некоторого центра O называется векторная сумма моментов импульсов всех точек системы относительно того же центра O.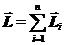 
(20.5)
|
|
|
Аналогично, момент всех сил, действующих на СМТ, определяется как векторная сумма моментов отдельных сил,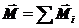 
. (20.6)
Отсюда, уравнение моментов для СМТ запишется так: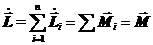 
. (20.7)
Скорость изменения момента импульса СМТ равна сумме моментов внешних сил. (Сумма моментов внутренних сил СМТ всегда равна 0).
5. Сохранение момента импульса СМТ. Если на систему материальных точек не действуют внешние силы, или действуют так, что сумма их моментов равняется нулю, то уравнение моментов принимает вид: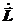 
= 0. Отсюда 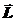= const. (20.8)
Момент импульса замкнутой (относительно моментов сил) СМТ есть величина постоянная.
Это закон сохранения момента импульса.
6. Законы сохранения. Важнейшими законами сохранения, справедливыми для любых изолированных систем, являются законы сохранения энергии, импульса, момента импульса и электрического заряда. В современной физике законы сохранения являются важной частью рабочего аппарата физической теории.
|
|
|
Например, закон сохранения энергии и открытие нейтрино, закон сохранения момента импульса и пульсары, и др.
В 1918 г. немецкий математик Эмми Нётер (1882 – 1935) сформулировала теорему, значение которой оказалось далеко выходящим за пределы алгебры, в рамках которой она была сформулирована. Суть теоремы в следующем.
Каждому закону сохранения физической системы соответствует определённый тип симметрии. Симметрия в физике понимается как инвариантность физических законов, которым подчиняется система, относительно некоторых преобразований входящих в эти законы величин. Наличие симметрии и приводит к тому, что для данной физической системы существует сохраняющаяся величина.
Современная физика рассматривает симметрии физических систем как симметрии пространства – времени, в котором движутся материальные тела. В результате законы сохранения вытекают из фундаментальных свойств материи.
Так, закон сохранения энергии вытекает из однородности времени. Действительно, если время однородно, то есть все его моменты эквивалентны, то изменение начала отсчета времени не может изменить энергию системы.
Закон сохранения импульса вытекает из свойства однородности пространства. Так как все точки пространства эквивалентны, то перенос (сдвиг) системы как целого в пространстве не изменяет импульса системы.
|
|
|
И, наконец, закон сохранения момента импульса вытекает из свойства изотропности пространства. Поворот системы как целого в пространстве в силу эквивалентности всех направлений не приводит к изменению момента импульса системы.
Более подробно связь законов сохранения со свойствами пространства-времени будет рассмотрена в курсе аналитической механики в 5 семестре.
Дата добавления: 2018-04-15; просмотров: 810; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!