Неинерциальные системы отсчета (НИСО). Силы инерции
1. Поступательно движущаяся НИСО. Наряду с инерциальными системами отсчёта, в которых выполняется первый закон Ньютона, могут существовать системы, в которых этот закон не выполняется. Это системы, движущиеся с ускорением. Их называют неинерциальными.
На тело m, находящееся в системе, движущейся поступательно с ускорением 
, действует в противоположном ускорению направлении сила инерции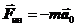 
(рис.32).
Если составляется уравнение движения тела m относительно НИСО, то в правой части помимо обычных сил – трения, упругости, гравитации и других – добавляется еще и сила инерции.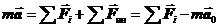 
. (15.1)
Здесь – ускорение, испытываемое НИСО.
2. Поступательно и вращательно движущаяся НИСО. Если система отсчета не только движется поступательно с ускорением , но ещё и вращается с угловой скоростью 
и угловым ускорением 
(4.9), а тело двигается относительно неё со скоростью 
, то
. (15.2)
Здесь 
– сила инерции, обусловленная неравномерностью поступательного движения НИСО,
– сила инерции, обусловленная неравномерностью вращения НИСО,
– центробежная сила инерции. Она обусловлена самим фактом вращения системы. Символ 
означает радиус – вектор, перпендикулярный оси вращения и проведённый от оси к материальной точке m.
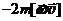– сила инерции Кориолиса. Здесь – скорость движения точки m относительно НИСО. Сила Кориолиса обусловлена одновременным действием фактов вращения системы и движения тела относительно системы.
|
|
|
Она может обращаться в нуль в 3-х случаях:
НИСО не вращается, = 0.
Тело m покоится относительно НИСО, = 0.
Тело движется по прямой, параллельной оси вращения НИСО. В этом случае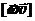 
=0
Решение задач в ИСО.
Пример 15.1. Шарик m с помощью нити длиной l закреплен на стержне вращающегося с угловой скоростью 
диска (рис.33). Найти угол отклонения нити a и силу натяжения нити Т.
Рассматривая движение в ИСО, мы оперируем только реальными силами. На шарик в ИСО действуют только две силы: сила тяжести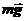 
и сила натяжения нити 
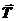. Под действием этих сил шарик движется по окружности радиуса 
= b + lsina. Уравнение движения шарика имеет вид:
. (15.3)
Спроектировав это уравнение на ось вращения и радиус вращения, и дополнив систему уравнений кинематическим выражением центростремительного ускорения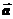 
, получаем систему из трёх уравнений с тремя неизвестными a, a, T.
(15.4)
Уравнения линейные, независимые, их число совпадает с числом неизвестных величин, поэтому система имеет единственное решение.
|
|
|
4. Решение задач в НИСО. Если рассматривать движение в НИСО, то в уравнение движения наряду с реальными силами добавляются силы инерции. Полагаем систему отсчета жестко связанной с диском. В этом случае при установившемся постоянном вращении шарик находится относительно системы отсчета в покое, так что = 0 (рис.34). Уравнение движения в НИСО принимает вид: 
. (15.5)
Из всех сил инерции отлична от нуля только центробежная сила,
.
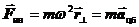Спроектировав уравнение движения на радиус вращения и на ось вращения, и добавив выражение для ускорения инерции, получаем систему из трех уравнений.
(15.6)
Система содержит 3 неизвестных величины – aцб, a, T – и имеет единственное решение. Полученная система уравнений равносильна системе, к которой мы пришли, решая задачу в ИСО. Таким образом, независимо от того, в какой системе отсчета рассматривается движение, решение задачи должно быть одним и тем же. Характер физического явления не зависит от способа его описания. (Очевидно, 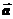цб = – 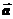, где 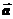– центростремительное ускорение. Ускорение 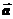цб есть в НИСО, а центростремительное ускорение 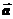– только в ИСО).
Дата добавления: 2018-04-15; просмотров: 1040; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!