Движение материальной точки под действием упругой силы, силы вязкого сопротивления среды и вынуждающей периодической силы

⇐ ПредыдущаяСтр 8 из 25Следующая ⇒

1.Вынужденные колебания. Это колебания, которые тело совершает при действии на него трёх сил: квазиупругой – kx, вязкого трения – hv_x и гармонической F_x= F₀cos W t, где F₀ – амплитудное значение действующей силы, W – её частота.

Уравнение движения тела имеет вид: m 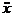= – kx – h 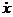+ F₀cos W t. (12.1)

Разделив всё на m и обозначив 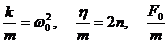= q, получаем:

qcos W t. (12.2)

Решение этого уравнения состоит из двух частей. Его первое слагаемое представляет собой общее решения уравнения (12.2) без правой части, которое описывает затухающие колебания системы в виде (11.3). Второе слагаемое, как частное решение неоднородного уравнения (12.2), описывает процесс установления вынужденных колебаний с частотой W .

x = Ae^–ntcos( t + j₀₁) + В(1 - e⁻^nt)cos(W t + j₀₂). (12.3)

Спустя время t >>t собственные колебания затухают, и первое слагаемое устремляется к нулю, а второе слагаемое выходит на стационарный режим x = Bcos(W t + j₀). (12.4)

Здесь амплитуда B = , (12.5)

а сдвиг по фазе j₀определяется из формулы: tgj₀ =- . (12.6)

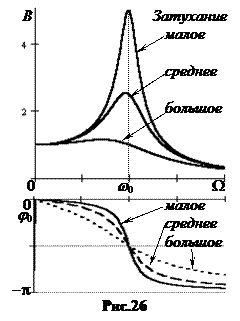2. Резонанс. Амплитуда вынужденных установившихся колебаний при t >>t не зависит от времени и пропорциональна амплитуде вынуждающей силы F₀(рис.26). Если исследовать функцию B(W) на экстремум, то можно найти значение W_p, при котором амплитуда вынужденных колебаний максимальна.

= 0, Þ

– w₀² + W_p² + 2n² = 0. (12.7)

Или W_p = . (12.8)

Максимальная амплитуда B_рез = B(W_p) = . (12.9)

Явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынуждающей силы приближается к частоте (при малом затухании это близко к частоте собственных колебаний) называется резонансом.

При малом затухании, когда n ® 0, B_p ® ¥, упругие деформации могут превысить допустимые и колебательная система разрушается.

При резонансе вынуждающая сила совершает максимальную работу по преодолению сил вязкого сопротивления среды. Когда резонансная амплитуда стабилизируется, работа вынуждающей силы полностью идёт на преодоление сил трения, механическая энергия системы остается постоянной.

При частоте вынуждающих колебаний много меньше собственной амплитуда вынужденных колебаний равна величине упругой деформации под действием амплитудной внешней силы F₀ , колебания совпадают по фазе, сдвиг фаз между ними j₀= 0.

При частоте вынуждающих колебаний много больше собственной амплитуда вынужденных колебаний стремится к нулевой величине, колебания происходят в противофазе, сдвиг фаз между ними j₀= p.

При частоте вынуждающих колебаний равной собственной (вблизи резонанса) вынужденные колебания отстают от вынуждающих на четверть периода, j₀= - p| 2.

3. Линейные и нелинейные колебательные системы. Если параметры колебательной системы – масса тела m, жёсткость пружины k, длина нити l и т.д. – остаются неизменными в процессе колебаний, сила трения линейно зависит от скорости, и квазиупругие силы линейно пропорциональны величине смещения, то колебательная система называется линейной, а колебания описываются линейными дифференциальными уравнениями. Строго говоря, линейные колебательные системы – это идеализация. В реальных колебательных системах силы достаточно сложно (не линейно) зависят от кинематических характеристик – смещения x и скорости v. Такие системы называются нелинейными. Однако, если эти зависимости выражены слабо, то в таких случаях реальная система приближённо может рассматриваться как линейная.

4. Автоколебания. В практике для возбуждения колебаний чаще применяется не гармоническая вынуждающая сила, а импульсная, действующая строго периодически в одной и той же фазе (рис.27). Работа этой силы при каждом её действии компенсирует потери энергии колебательной системы на трение в течение каждого периода действия силы.

Такие колебания, строго говоря, не являются гармоническими, но обладают постоянными периодом и амплитудой. Это - автоколебания, а системы, в которых они возникают, называются автоколебательными. Например, часы, свисток, качели, язычковые и духовые музыкальные инструменты.

5. Параметрическое возбуждение колебаний. Введение энергии в колебательную систему может осуществляться не только путём периодической силы, действующей на тело в направлении его движения, но и путём изменения одного из параметров колебательной системы. Так, если у математического маятника в фазах амплитудных отклонений удлинять нить, а в момент прохождения нити положения равновесия укорачивать её, то колебания будут периодическими и не затухающими (рис.28). Это параметрическое возбуждение колебаний.

Поскольку частота изменения параметра должна быть кратной частоте колебаний, то в параметрическом возбуждении колебаний есть сходство с резонансом, поэтому его называют часто параметрическим резонансом. Сама колебательная система является в этом случае нелинейной.

Закон всемирного тяготения

1. Законы Кеплера. В начале 17 века после обработки результатов многолетних наблюдений датского астронома Тихо Браге немецкий учёный Иоганн Кеплер установил 3 закона движения планет вокруг Солнца.

Первый закон,1609 г. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.

Второй закон, 1609 г. Радиус – вектор планеты в равные времена описывает равные площади.

Третий закон.1619 г. Квадраты времён обращения планет относятся как кубы больших полуосей эллиптических орбит, по которым они движутся вокруг Солнца.

2. Закон всемирного тяготения.Проанализировав законы Кеплера и опираясь на законы механики, Ньютон пришёл к закону всемирного тяготения, опубликованному в 1687 г. Логику рассуждений, приведших к открытию закона, можно представить по такой схеме. Полагаем для простоты траектории движения планет круговыми (для всех планет эксцентриситет эллиптических орбит очень мал, отношение полуосей близко к единице ). Если индекс 1 присвоить одной планете, например, Марсу, а индекс 2 – другой (Венере), то по 3-му закону Кеплера . (13.1)

В соответствии с законами динамики Ньютона планеты по круговым орбитам должны двигаться равномерно. Их линейные скорости и центростремительные ускорения равны . (13.2)

Но по 3-му закону Кеплера . Тогда . (13.3)

Итак, центростремительные ускорения, которые испытывают планеты, обратно пропорциональны квадратам их расстояний до Солнца. Величина центростремительной силы есть F = ma. Отношение сил равно . (13.4)

Следовательно, сила, с которой планета притягивается к Солнцу, пропорциональна массе планеты и обратно пропорциональна квадрату расстояния до Солнца. Но Солнце и планеты – физически равноправные тела. Поэтому, если сила пропорциональна массе планеты, то она должна быть пропорциональна и массе Солнца. F ~ 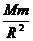. (13.5)

Но Ньютон идет дальше. Он экстраполирует закон взаимодействия между планетами и Солнцем на взаимодействие всех материальных объектов. Он приходит к идее закона Всемирного тяготения.

Любые два точечные тела притягиваются друг к другу с силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними (рис.29). . (13.6)

Здесь G – гравитационная постоянная. Численно она равна силе, с которой притягиваются две единичные точечные массы, находящиеся на единичном расстоянии друг от друга.

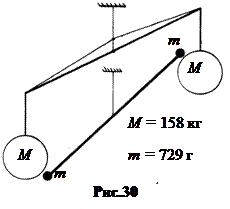3. Опыты Кавендиша. Первые прямые измерения гравитационной постоянной G были сделаны в 1798 г. английским учёным Генри Кавендишем (рис.30). Современное значение G = (6,6720 ± 0,0041)×10^–11 . Работы Кавендиша позволили ему оценить массу Земли: М_з = 6×10²⁴ кг, и вычислить среднюю плотность Земли r = 5,18×10³. (Современное значение r = 5,5×10³ ).

4. Гравитационное поле. Ньютон не «измышлял гипотез» о природе тяготения, он постулировал, что каждому телу присуща способность мгновенно воздействовать на другие тела на любом расстоянии. Эту концепцию назвали гипотезой дальнодействия.

Современная физика считает, что все взаимодействия осуществляются полями, то есть с участием «третьего» - посредника взаимодействия. Поле рассматривается как материальный объект, заполняющий пространство вокруг взаимодействующих тел. Наряду с гравитационным к настоящему времени известны ещё три вида фундаментальных взаимодействий: электромагнитное, сильное и слабое. Взаимодействия передаются полями с конечной скоростью. Современная физика пытается представить механизм действия поля как обмен особыми частицами, осуществляющими каждый вид взаимодействия.

Гравитационное поле характеризуется двумя величинами.

a. Напряженность, это силовая характеристика, вектор ; (13.7)

Напряжённость в точке гравитационного поля численно равна силе, с которой поле действует на тело единичной массы, помещённое в данную точку поля. На Земле напряженность гравитационного поля приблизительно равна ускорению свободного падения, но точно совпадает с ним по величине и направлению только на полюсах.

б. Потенциал, энергетическая характеристика, скаляр . (13.8)

Потенциал в точке гравитационного поля численно равен энергии единичной массы, помещенной в данную точку поля. Потенциал – нормируемая величина. Если считать энергию взаимодействия тел на бесконечности равной нулю, то потенциал гравитационного поля на расстоянии r от центра шарового тела есть . (13.9)

5. Гравитационная и инертная массы. Во втором законе динамики F = ma и законе всемирного тяготения (13.6) используются разные массы.

Во 2-м законе динамики масса есть мера инертности тела, это инертная масса m_a.. В законе тяготения масса есть мера способности тел притягиваться друг к другу. Это гравитационная, или тяжелая, масса m_G Формально тяжелая масса m_G подобна электрическому заряду тела, поэтому её называют ещё гравитационным зарядом.

При движении тел в поле тяготения в уравнение движения входят обе массы. Например, при свободном падении тел: m_a= , где 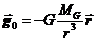– напряжённость гравитационного поля. Есть ли между массами различие или внутренняя связь, можно найти, сравнивая ускорения свободного падения различных тел, .

Впервые такой эксперимент провел Галилей в 1609 г. Он изучал падение разных тел с наклонной башни в городе Пизе. В итоге он установил, что все тела, независимо от вещества и массы, падают в поле силы тяжести Земли с одним ускорением (закон Галилея). Это значит, что инертная и тяжёлая массы пропорциональны между собой, а коэффициент пропорциональности одинаков для всех веществ.

Численное значение гравитационной постоянной G выбирается таким, чтобы этот коэффициент пропорциональности был равен единице, m_a = m_G. По современным данным эти массы совпадают с точность до 10^-¹³.

Дата добавления: 2018-04-15; просмотров: 780; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!