Применение формул размерности.
Поскольку размерность обеих частей любых равенств должна быть одинакова, то проверка размерностей используется как один из критериев правильности решения задач.
Перевод внесистемных величин в СИ и обратно через формулы размерности:
5 см2 = 5×(10-2 м)2 = 5×10-4 м2, 18 км| ч = 18×1000 м| 3600 с = 5 м| с.
Анализ размерностей позволяет устанавливать функциональные связи между физическими величинами по формулам размерности.
Анализ критериев подобия позволяет рационально планировать эксперимент и моделировать сложные процессы в лабораторных условиях.
См. напр.: Г. Хантли× Анализ размерностей. Мир× М.- 1970.
Колебательное движение материальной точки
1. Незатухающие колебания. Рассмотрим движение тела, прикрепленного к свободному концу пружины (рис.21). Полагаем, что трение отсутствует. Поскольку тело может двигаться только в направлении горизонтальной прямой (например, тело скользит по натянутой струне), то в отсутствие трения сила тяжести не влияет на характер движения. Если тело сместить от положения равновесия и предоставить само себе, то в любой момент времени на него действует лишь одна сила – сила упругости, направленная к положению равновесия. В проекции на ось ОХ уравнение движения принимает вид: 
, или
. (10.1)
Разделим обе части уравнения на m и введём обозначение k| m = w02. Тогда получим
. (10.2)
|
|
|
Это дифференциальное уравнение второго порядка с постоянными коэффициентами. Чтобы найти кинематический закон движения материальной точки, надо это уравнение проинтегрировать (2-я задача динамики).
Путем подстановки различных функций можно убедиться, что решением этого уравнения является гармоническая функция x(t)= Acos(w0t+j0). (10.3)
Амплитуда А и начальная фаза j0 определяются из начальных условий при t = 0:
x(0) = x0 = Acosj0;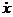 
(0) = v0 = –Aw0sinj0. (10.4)
Отсюда амплитуда колебаний 
; начальная фаза j0= arctg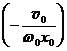 
.
Итак, материальная точка, движущаяся под действием одной лишь упругой силы, испытывает гармонические колебания с постоянной амплитудой и частотой w0= 
. Это незатухающие (свободные) колебания. Частота таких незатухающих колебаний w0 называется собственной частотой колебательной системы. Она определяется внутренними параметрами колебательной системы. В случае пружинного маятника – это масса груза m и жёсткость пружины k.
Гармонические колебания могут возникать не только под действием упругой силы, но и любой другой, пропорциональной смещению x и направленной к положению равновесия. Такие силы, определяющиеся общей формулой Fx = – kx, называются квазиупругими.
|
|
|
2. Энергия колебательной системы. Совокупность элементов, обеспечивающих колебательное движение тела, называют колебательной системой. Колебательную систему, в которой материальная точка совершает гармонические колебания, называют гармоническим осциллятором (или классическим осциллятором). Рассмотрим изменение кинетической и потенциальной энергии гармонического осциллятора.
а. Кинетическая энергия осциллятора есть энергия движения материальной точки,
Eк=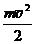 
. Так как v = 
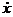= – Aw0sin(w0t + j0), то Eк= 
sin2(w0t + j0), или
Eк = 
. (10.6)
(Из формул тригонометрии: cos2a = 
(1 + cos2a), sin2a = (1 – cos2a) )
Кинетическая энергия гармонически колеблющегося тела изменяется с удвоенной частотой 2w0.
б. Потенциальная энергия осциллятора есть энергия упругой деформации пружины. Eп= 
. Так как x = Acos(w 0t + j0), то Eп= 
cos2(w0t + j0). Но k = mw02. Отсюда
Eп= cos2(w0t+j0) = 
. (10.7)
Потенциальная энергия гармонического осциллятора также изменяется по гармоническому закону с удвоенной частотой в противофазе по отношению к кинетической энергии (рис.22). Полная механическая энергия гармонического осциллятора E = Eк+ Eп = const или:
|
|
|
E = sin2(w0t+j0)+ cos2(w0t+j0) = . (10.8)
Когда колебания совершаются только под действием квазиупругих сил, полная механическая энергия осциллятора остаётся постоянной.
3. Математический маятник. Это идеализированная колебательная система, состоящая из точечной массы m, подвешенной в однородном гравитационном поле на невесомой и нерастяжимой нити длиной l (рис23).. Найдём кинематический закон движения математического маятника.
На массу m действуют две силы – сила тяжести m 
и сила натяжения нити 
. Сумма этих сил 
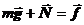направлена по касательной к дуге окружности, по которой может двигаться масса m. Запишем уравнение движения при его естественном задании: m 
= – f.
Но f = mg sina. Отсюда m = – mg sina. Смещение по дуге можно представить через угол a. Так как s = la , то при l =const (нить нерастяжимая) = l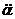 
, и уравнение движения в переменных a и t принимает вид: 
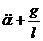sina = 0. (10.9)
Если ограничиться малыми углами, то при a < 4° sina @ a cточностью до трёх знаков. В этом случае уравнение движения упрощается: 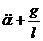a = 0. (10.10)
Но это – уравнение незатухающих гapмонических колебаний. Кинематический закон колебаний, выраженный через угловое смещение, имеет такой же вид, как и закон колебаний груза на пружине. a = Аcos(w0t+j0). (10.11)
|
|
|
Здесь А – амплитудный угол отклонения нити, j0 – начальная фаза колебаний.
Циклическая частота колебаний математического маятника аналогично пружинному 
. Период колебаний T0= 
. (Формула Гюйгенса, I673). (10.12)
Период колебаний не зависит от амплитуды (изохронность колебаний). Колебания изохронны лишь при малых углах отклонения маятника от положения равновесия a < 4°.
Дата добавления: 2018-04-15; просмотров: 438; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!