Движение точки по прямой и по окружности

1. Прямолинейное движение. Если траектория точки - прямая линия, то говорят, движение точки прямолинейно. Для описания движения в этом случае достаточно одной координатной оси, которую располагают вдоль по траектории. Координатный и естественный способы задания движения в этом случае совпадают.

В практике наиболее важны два случая - равномерного и ускоренного движения.

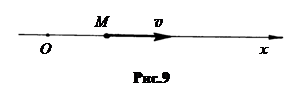а. Равномерное движение (рис.9). Скорость vпостоянна по величине и по направлению, v= const.Или в проекции: v_x= const.. Кинематический закон равномерного движения имеет вид: x = x₀ +v_xt.               (4.1)

Начальная координата точки x₀ и проекция скорости v_x могут иметь знак "плюс" или "минус".

б. Ускоренное движение. Скорость изменяется со временем. Пусть ускорение точки есть a, в проекции на ось a_x. Тогда скорость в любой момент времени найдется интегрированием: v_x = òa_xdt + v₀.                                                                                   (4.2)

При постоянном ускорении, a_x= const, получаем скорость точки в равноускоренном движении: v_x = v₀+a_xt.                                                                                                    (4.3)

После второго интегрирования находим закон равноускоренного движения:

x=x₀+ 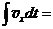x₀+v₀t+ 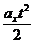.                                                                                     (4.4)

Знак числа x₀определяется положением точки на координатной оси в начальный момент времени. Справа от точки отсчета - знак "плюс", слева - знак "минус". Знаки чисел v₀ и a_x определяются знаками проекций соответствующих векторов на ось ОХ. Если вектор vили aсовпадает по направлению с осью OX - знак "плюс", если противоположен - знак "минус".

2. Движение точки по окружности. Наиболее наглядно векторное представление этого движения (рис.10). Здесь С - центр окружности,r - радиус-вектор, проведенный из центра окружности в движущуюся точку М,  v- скорость движения точки М.

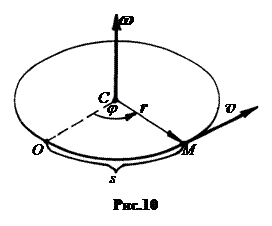Угловую скорость вращения радиуса - вектора удобно показать вектором угловой скорости w. Модуль вектора w равен производной угла поворота радиуса по времени, w = 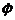, а направление w совпадает с поступательным движением правого винта. Все три вектора r, w и v однозначно связаны между собой: 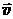= [ 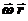]. (4.5)

Вектор w перпендикулярен плоскости траектории, поэтому угол w ^ r = 90°, и v =w r sin(w ^r)=w _.r.                                                (4.6)

Найдем ускорение точки М.

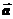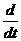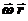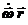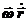= = [ ] = [ ] +[ ] .   (4.7)

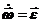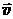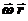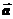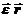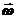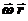Производная угловой скорости по времени есть угловое ускорение, , а производная радиуса-вектора - вектор скорости, = = [ ]Þ   = [ ] + [ [ ]]     .           (4.8)

Раскроем двойное векторное произведение.

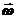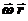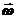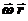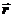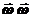[ [ ]] = ( ) - ( ) =-w² 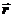.      Итак: 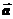= [ 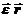]-w² 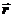.                   (4.9)

Член [ 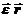] =   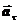- касательное ускорение. Оно или сонаправлено или противоположно по направлению вектору скорости точки   .

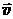Член -w² 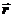  - центростремительное ускорение. Оно перпендикулярно вектору скорости 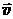, следовательно, перпендикулярно касательной к траектории. Поэтому его называют нормальным ускорением, -w² 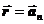. Вектор полного ускорения равняется сумме касательного и нормального ускорений: 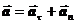.                                               (4.10)

Очевидно, модуль полного ускорения a = 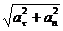.                                    (4.11)

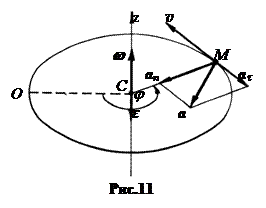
Если точка в своем движении по окружности проходит расстояние, большее длины окружности, то её смещение по траектории от точки отсчета циклично. Записывать закон движения через смещение в этом случае чревато путаницей. Удобнее закон движения точки по окружности представлять через угол, для которого цикличность естественна (рис.11):

Если точка движется по окружности равномерно, то j = j₀+w t.               (4.12)

При ускоренном движении j =j₀+w₀ t + 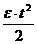. (4.13)

Вращательное движение характеризуется ещё такими параметрами:

а. Частота вращения n. Она равна числу оборотов радиуса-вектора в секунду. Единица n - герц, 1 Гц = 1 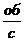, n = 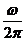.              (4.14)

б. Период вращения Т. Это время одного оборота радиуса-вектора T = 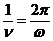.            (4.15)

Колебательное движение точки

1.Колебаниями можно назвать в механике любые движения тел в ограниченном пространстве. Если через равные промежутки времени движение повторяется во всех деталях, колебания называют периодическими, если нет - апериодическими.

Наиболее важны гармонические колебания, при которых смещение движущейся точки от положения отсчета изменяется по закону синуса или косинуса.

2. Закон гармонического колебательного движения  x = Acos(w t+j₀).       (5.1)

Здесь А - амплитуда колебаний, w = 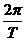 - циклическая частота, Т- период колебаний, w t+j₀- фаза колебаний, угловая величина, определяющая положение точки на траектории.

Найдем скорость и ускорение гармонически колеблющейся точки.

v = 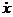= - Aw sin(w t + j₀) = - v_maxsin(w t + j₀).                                                      (5.2)

a = 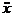= - Aw²cos(w t+j₀) = - a_maxcos(w t+j₀).                                                         (5.3)

3. Сложение колебаний, совершающихся вдоль одной прямой, можно сделать методом векторных диаграмм (рис.12).

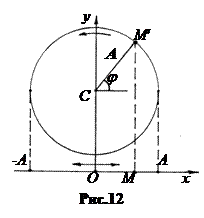Гармоническое колебание точки вдоль оси ОХ интерпретируется как проекция конца вектора, вращающегося в плоскости ХОУ с угловой скоростью w. Вектор А - условный вектор, длина его равна амплитуде колебаний точки.

Различают два случая:

а. частоты колебаний одинаковы,

б. частоты колебаний различны.

а. Cложение колебаний с одинаковыми частотами (рис.13). 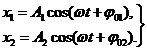                                       (5.4)

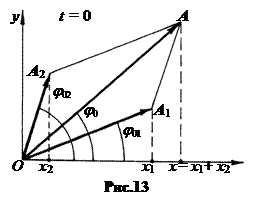Суммарное колебание есть также гармоническое. Действительно, w₁=w₂=w, и весь векторный параллелограмм вращается как одно целое. Амплитуда суммарного колебания A= 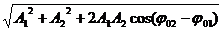,            (5.5)

а начальная фаза найдется из формулы: 

tgj₀ = 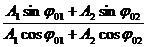.                      (5.6)

Итак, x=x₁ + x₂ = Acos(w t +j₀).                             (5.7)

---

Дата добавления: 2018-04-15; просмотров: 848; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!