Движение материальной точки под действием упругой силы и силы вязкого сопротивления среды

1. Уравнение затухающих колебаний. В реальных условиях невозможно сделать колебательную систему, в которой бы не было трения.

Рассмотрим колебания в системе, в которой сила трения пропорциональна скорости движения тела, т.е. , где h – коэффициент вязкого сопротивления среды. Уравнение движения в проекции на ось ОХ принимает вид: =– kx – hv.         (11.1)

Так как v = , обозначив k| m = w₀², h| m =2n, получаем: . (11.2)

Общий вид решения этого уравнения зависит от соотношения между коэффициентами w₀ и n.

2. Затухающие периодические колебания. Пусть сила упругости больше силы вязкого сопротивления среды, так что w₀ > n. Решение уравнения в этом случае имеет вид:

x = A₀e^–ntcos(w t+j₀), где w = ,                                                                   (11.3)

A₀ – амплитуда в начальный момент времени t =0.

Произведение A₀e^–nt = A₀exp(-t|t) = A(t) - можно интерпретировать как амплитуду, зависящую от времени. Величина t = 1| n - время релаксации колебательной системы, за которое амплитуда колебаний убывает в е раз. Таким образом, колебание тела в вязкой среде при w₀ > n с некоторой нестрогостью можно характеризовать как колебания периодические (тело периодически проходит через положение равновесия) с постоянной частотой w =  и экспоненци-ально убывающей амплитудой (рис.24). Период затухающих колебаний больше периода свободных колебаний,

T = = Т₀.

Скорость затухания колебаний определяют декрементом затухания b, равным отношению любого смещения к тому, которое последует через период.

b = 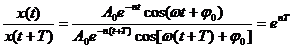.                                      (11.4)

За каждый период T амплитуда и любое смещение убывают в одно и то же число раз, равное b = e^nT. Натуральный логарифм этого числа lnb = nT = d                      (11.5)

называют логарифмическим декрементом затухания. Величину n = h| 2m называют иногда коэффициентом или показателем затухания.

Если N =t|T - число колебаний, которое система совершает в течение времени релаксации t, соответствующее уменьшению амплитуды в e раз, то NnT= Nd = nt = 1. (11.6)

Добротность системы Q = pN равна разности фаз колебаний, соответствующей уменьшению энергии колебательной системы в е раз.

3. Затухающие апериодические колебания. Если силы трения настолько велики, что w₀< n, то функция, описывающая колебания, уже не является периодической. Колебания при больших силах трения неповторяющиеся. Колеблющееся тело проходит через положение равновесия не более одного раза (рис.25).

1.    x₀≠0, v₀ = 0.

2.    x₀≠0, v₀≠0.

3.    x₀ = 0, v₀≠0.

Такие колебания называют апериодическими (частица а – заимствована из греческого, означает отрицание).

4. Диссипация энергии. При затухающих колебаниях механическая энергия системы постепенно переходит в тепло, во внутреннюю энергию системы. Говорят, происходит диссипация энергии. Полная механическая энергия системы E = E_к+ E_п = 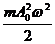e^–2nt. (11.7)

Энергия системы пропорциональна квадрату амплитуды. За время релаксации энергия убывает в е² раз, за период энергия убывает в b ² раз. 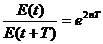= b ².            (11.8)

Добротность системы Q = 2pE|DE пропорциональна отношению полной энергии системы к величине потерь её за один период колебаний.

---

Дата добавления: 2018-04-15; просмотров: 463; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!