Проявление сил инерции на Земле
1. Линия отвеса. Если рассматривать Землю как однородный вращающийся шар, то на массу m находящуюся неподвижно на поверхности Земли, в системе отсчета, связанной с Землёй, действуют две силы: одна – сила притяжения Земли, направленная к её геометрическому центру, другая – центробежная сила инерции, направленная перпендикулярно к оси вращения Земли (рис.35).
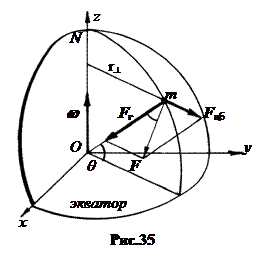 Вектор суммарной силы – будем называть её силой тяжести – не совпадает с радиусом Земли; он отклоняется от него на угол a, величина которого зависит от широты местности q.
Вектор суммарной силы – будем называть её силой тяжести – не совпадает с радиусом Земли; он отклоняется от него на угол a, величина которого зависит от широты местности q.
По теореме синусов 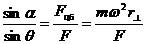 . (16.1)
. (16.1)
Направление суммарной силы есть направление вектора ускорения свободного падения на вращающейся Земле. sina=sinq  . (16.2)
. (16.2)
Направление вектора F определяет линию отвеса, или геодезическую вертикаль. Здесь r – радиус Земли.
Величина ускорения свободного падения максимальна на полюсе: gп= 9,832 м|с2и минимальна на экваторе: gэ= 9,780 м|с2.
В городе Кирове q @ 58,5°. Ускорение свободного падения g = 9,817 м|с2. Линия отвеса в городе Кирове проходит от геометрического центра Земли на расстоянии около 10 км.
2.Вес тела. Весом тела P называют силу, с которой тело действует на опору (или подвес), удерживающие тело в покое относительно этой опоры. 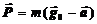 ). (16.3)
). (16.3)
 Здесь g0=-G
Здесь g0=-G 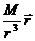 – напряженность гравитационного поля, иначе, ускорение, с которым тело падало бы на невращающейся Земле;
– напряженность гравитационного поля, иначе, ускорение, с которым тело падало бы на невращающейся Земле;  – ускорение, испытываемое подставкой.
– ускорение, испытываемое подставкой.
Например, подставка покоится на поверхности Земли. Тогда 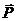 =m(
=m( 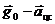 ),
),
|
|
|
где 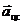 – центростремительное ускорение, испытываемое подставкой в результате вращения Земли. Очевидно,
– центростремительное ускорение, испытываемое подставкой в результате вращения Земли. Очевидно, 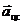 =
= 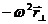 , и
, и 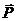 =m(
=m( 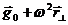 ).
).
Если подставка свободно падает, то  =
= 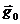 , и
, и 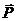 =0. Тело также свободно падает, говорят, оно находится в состоянии невесомости.
=0. Тело также свободно падает, говорят, оно находится в состоянии невесомости.
Если a>g0, то чем больше ускорение, с которым движется подставка, тем больше вес.
Сила тяжести приложена к телу, а вес – к подставке. Сила тяжести не зависит от движения тела, а вес – зависит.
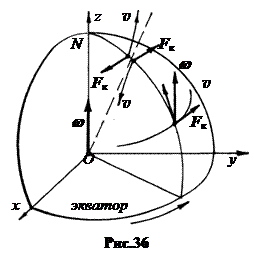
3. Маятник Фуко. При движении тела со скоростью  относительно Земли на тело кроме центробежной силы инерции
относительно Земли на тело кроме центробежной силы инерции 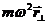 действует еще сила Кориолиса
действует еще сила Кориолиса 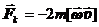 . Если тело свободно падает, то под действием силы Кориолиса оно отклоняется от вертикали на восток. Если тело взлетает вверх, то оно отклоняется от вертикали на запад (рис.36).
. Если тело свободно падает, то под действием силы Кориолиса оно отклоняется от вертикали на восток. Если тело взлетает вверх, то оно отклоняется от вертикали на запад (рис.36).
 Если тело движется по поверхности Земли, то сила Кориолиса стремится сместить его в северном полушарии вправо, а в южном – влево. В результате реки в северном полушарии подмывают правый берег, а в южном – левый. Этот факт известен в географии как закон Карла Бэра (русский естествоиспытатель, 1792–1876 г.г.).
Если тело движется по поверхности Земли, то сила Кориолиса стремится сместить его в северном полушарии вправо, а в южном – влево. В результате реки в северном полушарии подмывают правый берег, а в южном – левый. Этот факт известен в географии как закон Карла Бэра (русский естествоиспытатель, 1792–1876 г.г.).
Если тело подвешено на нити и совершает маятниковые колебания, то систематическое действие силы Кориолиса поворачивает плоскость качаний маятника относительно Земли с угловой скоростью wsinq , где q – географическая широта места (рис.37). Этот факт явился прямым доказательством вращения Земли вокруг своей оси. Реальный опыт поставил в 1850 г. француз Леон Фуко в Парижской обсерватории.
|
|
|
Задание. Выяснить, проявляется ли и, если да, то как, сила Кориолиса при движении тела по экватору с запада на восток и с востока на запад?
4. Сила инерции является частным случаем сил гравитационного поля, понимаемого в таком расширенном смысле. Общая теория относительности, или релятивистская теория гравитации, устанавливает уравнения гравитационного поля. Они называются уравнениями Эйнштейна. Закон всемирного тяготения Ньютона содержится в уравнениях Эйнштейна и верен только приближенно. Приближенный характер закона всемирного тяготения, впрочем, следует уже из того, что в основе этого закона лежит представление о мгновенном распространении взаимодействий, атакое представление имеет ограниченную область применимости.
Ввернемся к вопросу об инерциальных системах отсчета. Пусть тело А настолько удалено от Солнечной системы, что ее гравитационным полем можно пренебречь, Тогда еще нельзя утверждать, что оно не подвержено действию никаких гравитационных полей. Мы не можем утверждать, что во Вселенной нет удаленных тел, создающих в месте нахождения тела А гравитационное поле g конечной напряженности. Убывание гравитационного поля из-за расстояния до этих тел может быть компенсировано возрастанием их масс. Однако если изучаются явления в ограниченной области пространства S, то при не слишком больших размерах ее поле g может считаться однородным. Тогда если тело А свободно падает в гравитационном поле g, то это поле будет полностью компенсировано поступательными силами инерции. Если тело А и не вращается (относительно удаленных масс), то оно не будет подвержено действию и остальных сил инерции. Система отсчета, связанная с таким невращающимся свободно падающим телом А, и будет инерциальной системой отсчета. Во всякой системе отсчета А’, вращающейся или движущейся ускоренно относительно системы А, появятся силы инерции. Но это движение есть не движение в "абсолютном пространстве", а движение относительна удаленных тел Вселенной. С этой точки зрения, принадлежащей австрийскому физику Эрнесту Маху (1838-1916), силы инерции возникают из-за вращений и ускоренных движений координатных систем относительно удаленных тел Вселенной. Это утверждение известно под названием принципа Маха.
|
|
|
Одно время точка зрения Маха казалась очень привлекательной. Ее в принципе разделял в первоначальных работах Эйнштейн. Однако в дальнейшем он от нее отошел. В современных космологических теориях принцип Маха не используется. Ввиду конечной скорости распространения взаимодействий всякое движение или изменение удаленных тел Вселенной может повлиять на процессы вблизи Земли не раньше чем через время. затрачиваемое светом на прохождение расстояния от этих тел до Земли. Принцип Маха этого не учитывает. Он не принимает во внимание силовые поля, существующие в галактическом и межгалактическом пространствах.
|
|
|
Дата добавления: 2018-04-15; просмотров: 1102; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
