Примеры действия законов сохранения. Удар шаров
1. Абсолютно неупругое соударение. В качестве иллюстрации использования законов сохранения импульса и энергии для решения задачрассмотрим соударение двух шаров.
При абсолютно неупругом соударении тела после соударения остаются в деформированном состоянии и слипаются. (Например, два пластилиновых куска). Ограничимся случаем центрального удара шаров, когда их центры масс движутся вдоль одной прямой (рис.41).
При неупругой деформации тел часть их механической энергии превращается во внутреннюю энергию, в результате закон сохранения механической энергии не выполняется. Выполняется только закон сохранения импульса. Сумма импульсов до удара равна сумме импульсов после удара.
. (19.1)
Из уравнения сохранения импульса можно найти любую из неизвестных величин. Например, скорость соединившихся после удара шаров: 
. (19.2)
Если шары двигаются в разные стороны или друг за другом так, что соударения не происходит, то и в этом случае формула (19.2) определяет скорость v движения центра масс системы из двух шаров. Если импульсы сближающихся шаров одинаковы, то их скорость после удара обращается в нуль (проекции импульсов шаров до удара одинаковы по величине, но противоположны по знаку). В этом случае вся кинетическая энергия шаров расходуется на их деформацию и превращается в тепло.
Если импульсы сближающихся шаров неодинаковы, то после удара соединившиеся шары будут двигаться в ту или иную сторону со скоростью v. В этом случае не вся кинетическая энергия шаров будет "исчезать", а только часть её.
|
|
|
Чтобы определить количество кинетической энергии, превратившейся в результате абсолютно неупругого удара в другие формы немеханической энергии (например, в тепло – при соударении макротел, в энергию излучения – при соударении элементарных частиц, и т.д.), удобно использовать систему отсчета, связанную с центром масс соударяющихся тел.
В такой системе отсчета тела после соударения покоятся. Значит, вся кинетическая энергия, которой обладали в этой системе тела до соударения, превращается в немеханические формы. Поэтому задача сводится к тому, чтобы определить скорость тел до соударения в системе центра масс.
Для этого достаточно из скоростей v01 и v02 вычесть скорость (19.2) движения центра масс v (преобразования Галилея для скоростей). Обозначим скорости шаров в системе центра масс vC1 и vC2. 
. (19.3)
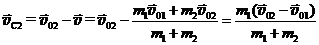. (19.4)
Подставив эти скорости в формулу кинетической энергии, получаем:
EК1 = 
; EК2 = 
. (19.5)
|
|
|
EК2 + EК1 =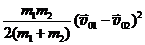 
; 
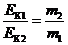. (19.6)
2. Абсолютно упругое соударение. Это другой предельный случай, когда механическая энергия системы тел полностью сохраняется. После удара тела расходятся, поэтому задача усложняется тем, что определять нужно скорость движения не одного, а двух тел. Поэтому приходится использовать оба закона сохранения.
Сохранение импульса: 
. (19.7)
Сохранение механической энергии: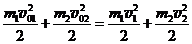 
. (19.8)
Сгруппируем члены обоих уравнений по массам шаров m1 и m2.
(19.9)
Второе уравнение можно развернуть ещё так: 
.
Разделив это уравнение на 1-е, получаем вспомогательное выражение, с помощью которого найдем скорости v1 и v2: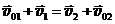 
. (19.10)
Умножим уравнение (19.9) на m2 и вычтем результат почленно из 1-го уравнения системы (19.8):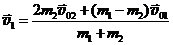 
. (19.11)
Умножим уравнение (19.10) на m1 и сложим с 1-м уравнением системы (19.9).
. (19.12)
|
|
|
Рассмотрим частные случаи.
а. Сталкиваются шары равных масс, m1 = m2 = m. В этом случае
v1 = v02 , v2 = v01 , шары обмениваются скоростями. (19.13)
б. Соударение шара со стенкой. Пусть m2 – масса стенки, полагаем m2 >> m1 . В этом случае v2 = v02 – скорость движения стенки, практически не изменяющаяся при ударе.
. (19.14)
Итак, скорость упруго ударившегося о стенку шара изменяется по величине на удвоенную скорость стенки. Этот вывод позволяет объяснить изменение температуры газа при его сжатии или расширении.
Если газ расширяется, например, поршень выходит из цилиндра, в котором находится газ, то молекулы ударяются с "убегающим" поршнем. Скорости молекул уменьшаются по величине на удвоенную скорость поршня. Средняя кинетическая энергии молекул газа падает, его температура снижается.
При сжатии все происходит наоборот. Скорость молекул, сталкивающихся с приближающимся поршнем, увеличивается, температура газа растет.
Дата добавления: 2018-04-15; просмотров: 464; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!