Система материальных точек. Теорема о движении центра масс. Закон сохранения импульса
1. Совокупность тел, которые взаимодействуют между собой и могут рассматриваться в данном движении как материальные точки, называется системой материальных точек. На каждую i-тую частицу системы из n материальных точек (СМТ) действуют силы как со стороны других частиц системы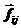 
– это внутренние силы, так и со стороны тел, находящихся вне данной системы, 
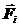– это внешние силы.
Чтобы знать движение СМТ в целом, нужно знать движение каждой частицы в отдельности. Если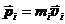 
– импульс i-той частицы, то движение СМТ определяется системой уравнений: 
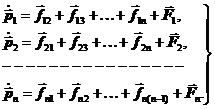(17.1)
2. Теорема о движении центра масс.Математическое исследование движения СМТ можно упростить, если просуммировать уравнения движения. При этом, согласно 3-му закону Ньютона, для каждых двух частиц системы сумма сил, с которыми они взаимодействуют, равна нулю: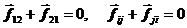 
. Но это значит, что сумма всех внутренних сил обращается в нуль. Отсюда 
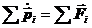. (17.2)
Преобразуем левую часть.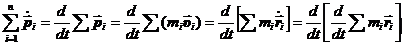 
.
Сумму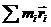 
можно представить так: 
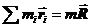, где m= 
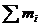– масса всех частиц системы, а 
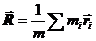– радиус-вектор некоторой воображаемой точки С, называемой центром масс СМТ. Отсюда
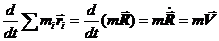, где 
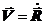– скорость движения центра масс системы. Уравнение движения СМТ принимает вид: 
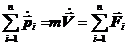. (17.3)
Центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила равна геометрической сумме всех внешних сил, действующих на частицы системы. Это теорема о движении центра масс.
|
|
|
Пример: центр масс осколков снаряда, разорвавшегося в воздухе, продолжает движение по той же траектории, по которой двигался бы неразорвавшийся снаряд.
3. Закон сохранения импульса. Рассмотрим движение системы материальных точек, в которой действуют только внутренние силы. Такие СМТ называются замкнутыми. Сумма внешних сил в этом случае равна нулю, а уравнение движения СМТ принимает вид:
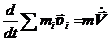= 0, Þ 
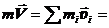const. (17.4)
Импульс замкнутой СМТ остаётся неизменным как по величине, так и по направлению. Это закон сохранения импульса замкнутых систем. Центр масс системы в этом случае движется прямолинейно и равномерно.
Под действием только внутренних сил в СМТ может происходить лишь обмен импульсами между отдельными её частицами, но невозможно изменение, возникновение или уничтожение импульса СМТ в целом.
4. Динамика тела переменной массы. Уравнение Мещерского. В качестве примера проявления закона сохранения импульса рассмотрим движение тела переменной массы.
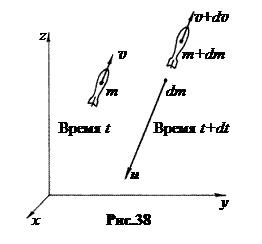Пусть в ИСО движется ракета массы m со скоростью v (рис.38). Импульс ракеты есть mv. Если в течение времени dt ракета отбросила массу газа dm, то в силу закона сохранения импульса она получает приращение скорости dv. Если скорость отбрасываемых газов относительно системы отсчета есть u, то закон сохранения импульса для системы тел ракета – газ запишется так:
|
|
|
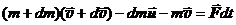. (17.5)
Здесь F– вектор внешних сил. Масса dm рассматривается в общем виде как приращение функции, поэтому в скобках берётся со знаком "плюс". Раскрыв скобки, получаем: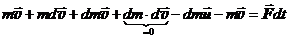 
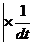, Þ
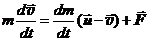. Уравнение Мещерского, 1897. (17.6)
Член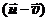 
есть скорость истечения газов относительно ракеты, 
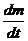– скорость изменения массы ракеты.
В правую часть равенства входят две силы. Это внешняя сила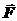 
и сила 
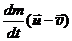, называемая реактивной.
Уравнение Мещерского является обобщением уравнения Ньютона на тела переменной массы. Оно переходит во 2-й закон Ньютона, когда масса тела остается постоянной, m = const, следовательно, 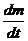= 0 и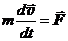 
.
| Мещерский Иван Всеволодович (I859–I935) – советский учёный в области теоретической и прикладной механики. В I9II г. написал использующийся до сих пор сборник задач по теоретической механике.
 Мы поможем в написании ваших работ! |