Упругие деформации твердых тел
1. Виды деформаций. Реальные твердые тела не являются абсолютно твердыми. В результате физических воздействий они изменяют свои размеры и форму, говорят – деформируются. Деформации бывают:
а. механические – при механическом воздействии тел,
б. тепловые – при изменении температуры тел,
в. электрострикционные – при изменении электрических полей,
г. магнитострикционные – при изменении магнитных полей.
Различают упругие деформации, когда форма и размеры ТТ восстанавливаются после прекращения внешнего воздействия, и неупругие, когда изменения остаются.
Самыми простыми деформациями являются:
–деформации растяжения и сжатия,
–деформации сдвига.
Сложные деформации изгиба и кручения сводятся к простым.
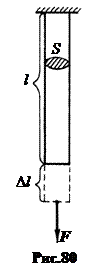
2. Сжатие и растяжение. Как установил Роберт Гук, удлинение цилиндрического образца пропорционально действующей на образец силе F, его длине l и обратно пропорционально площади сечения образца S (рис.80). 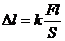 . Закон Гука, 1660г. (27.1)
. Закон Гука, 1660г. (27.1)
 Коэффициент пропорциональности k называют иногда коэффициентом растяжения. Томас Юнг предложил в 1807г. пользоваться обратной величиной Е = 1çk. Впоследствии величину Е назвали модулем упругости, или модулем Юнга.
Коэффициент пропорциональности k называют иногда коэффициентом растяжения. Томас Юнг предложил в 1807г. пользоваться обратной величиной Е = 1çk. Впоследствии величину Е назвали модулем упругости, или модулем Юнга.
Отношение 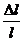 = e называют относительной деформацией растяжения или сжатия, а отношение силы к сечению
= e называют относительной деформацией растяжения или сжатия, а отношение силы к сечению 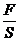 =s – нормальным напряжением. Закон Гука принимает в таких обозначениях лаконичную форму:
=s – нормальным напряжением. Закон Гука принимает в таких обозначениях лаконичную форму: 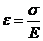 . (27.2)
. (27.2)
|
|
|
Модуль Юнга Е численно равняется нормальному напряжению, при котором длина образца изменилась бы вдвое. (При s = E 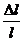 = e = 1.) Реальные материалы, за исключением каучуков и резин, не позволяют осуществить такую деформацию, поскольку разрушаются при значительно меньших напряжениях.
= e = 1.) Реальные материалы, за исключением каучуков и резин, не позволяют осуществить такую деформацию, поскольку разрушаются при значительно меньших напряжениях.
3. Коэффициент Пуассона. При деформациях происходит изменение объема тел. Если r – радиус цилиндрического образца, то 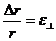 – поперечное сжатие (уширение) образца. В 1810г. французский ученый Симеон Пуассон предложил характеризовать изменение объема отношением поперечного сжатия к продольной деформации, то есть величиной
– поперечное сжатие (уширение) образца. В 1810г. французский ученый Симеон Пуассон предложил характеризовать изменение объема отношением поперечного сжатия к продольной деформации, то есть величиной 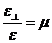 , которую называют коэффициентом Пуассона.
, которую называют коэффициентом Пуассона.
Если объем материала не меняется, то m = 0,5 (например, жидкость или каучуки). Действительно, объем недеформированного образца V1 = pr2l. После деформации объем образца V2 = p(r – Dr)2(l + Dl). При неизменяющемся объеме V2 – V1 = 0. Приравняв правые части и пренебрегая величинами второго порядка малости (т.е. выбросив величины Dr2 и DrDl), получаем: V2 – V1 = pr2Dl – 2prlDr = 0. Отсюда 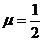 . (
. ( 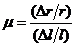 ).
).
Все реальные ТТ увеличивают объем при растяжении и уменьшают его при сжатии, поэтому коэффициент Пуассона у них меньше 1ç2.
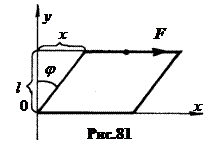 4. Деформация сдвига (рис.81). Закон Гука для деформации сдвига имеет вид:
4. Деформация сдвига (рис.81). Закон Гука для деформации сдвига имеет вид: 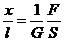 или
или 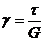 . (27.3)
. (27.3)
|
|
|
 Здесь F – сила, касательная поверхности образца,
Здесь F – сила, касательная поверхности образца, 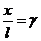 относительная деформация сдвига, а
относительная деформация сдвига, а 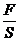 =t – касательное напряжение, G – модуль сдвига. Численно он равен касательному напряжению t, при котором угол сдвига составил бы 45°.
=t – касательное напряжение, G – модуль сдвига. Численно он равен касательному напряжению t, при котором угол сдвига составил бы 45°.
Модуль упругости при растяжении (модуль Юнга) Е и модуль сдвига G в пределах применимости закона Гука связаны соотношением: 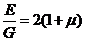 . (27.4)
. (27.4)
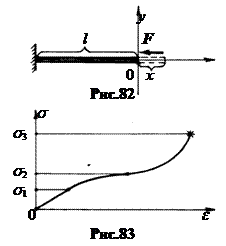
5. Энергия деформированного тела. Потенциальную энергию W упруго деформированного тела можно найти, вычислив работу, которую совершает упруго деформированное тело после снятия внешнего напряжения (рис.82).
 A = W =
A = W = 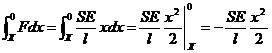 . (27.5)
. (27.5)
Отсюда W = 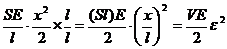 . (27.6)
. (27.6)
Плотность энергии 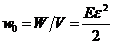 . (27.7)
. (27.7)
Аналогично находится плотность потенциальной энергии при деформации сдвига: 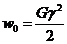 . (27.8)
. (27.8)
 6. Гистерезис. Пределы упругой деформации большинства материалов (за исключением резин и каучуков) очень невелики. При увеличении напряжения s относительная деформация e изменяется, как показано на рис.83. Здесь s1 – предел упругости, s2 – предел текучести, s3 – предел прочности.
6. Гистерезис. Пределы упругой деформации большинства материалов (за исключением резин и каучуков) очень невелики. При увеличении напряжения s относительная деформация e изменяется, как показано на рис.83. Здесь s1 – предел упругости, s2 – предел текучести, s3 – предел прочности.
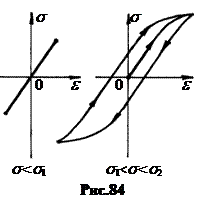
 Если образец подвергнуть воздействию периодической силы, то в зависимости от величины напряжения s график изменения относительной деформации e выглядит по-разному (рис.84). График называется петлей гистерезиса (греч. hysteresic –: отставание). Чем больше площадь петли гистерезиса, тем большая часть работы идет на не обратимые пластические деформации, тем сильнее нагревается образец.
Если образец подвергнуть воздействию периодической силы, то в зависимости от величины напряжения s график изменения относительной деформации e выглядит по-разному (рис.84). График называется петлей гистерезиса (греч. hysteresic –: отставание). Чем больше площадь петли гистерезиса, тем большая часть работы идет на не обратимые пластические деформации, тем сильнее нагревается образец.
|
|
|
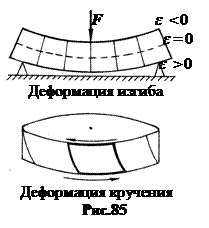
7. Сложные деформации. Деформация изгиба сводится к деформациям сжатия и растяжения, а деформация кручения – к деформации сдвига (рис.85).
Для уменьшения деформаций конструкционных элементов – балок, опор и др. – и экономии материала, что позволяет в то же время уменьшить массу конструкций, им придается различный сложный профиль (рис.86).
ГЛАВА 3. ЖИДКОСТИ И ГАЗЫ
Дата добавления: 2018-04-15; просмотров: 609; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
