Колебания в упругой среде. Волны
1. Сжимаемость жидкостей и газов.Реальные жидкости и газы сжимаемы, то есть под действием внешней силы могут уменьшать свой объем. Наиболее заметна их сжимаемость при скоростях движения тел или частиц среды, близкой к скорости звука в данной среде.
Если в какой-то точке сплошной упругой среды тело или частица среды колеблются около положения равновесия, то их колебания передаются другим частицам среды. В результате в среде распространяется волна. Кинематическим признаком волнового движения является распространение фазы колебаний, динамическим – перенос энергии.
2. Волновая поверхность. Геометрические виды волн. Воображаемая поверхность, в каждой точке которой частицы среды колеблются в одной фазе, называется волновой поверхностью. В зависимости от формы волновой поверхности различают плоские, сферические и цилиндрические волны.
а. Плоская волнаизлучается (генерируется) колеблющейся плоской поверхностью (рис.106). Если стенка колеблется по гармоническому закону x = Acosw t, (31.1)
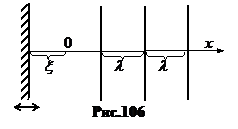где x – смещение стенки относительно положения равновесия вдоль оси ОХ, то колебания частиц среды будут отставать по фазе в зависимости от расстояния до стенки X. Время отставания t¢=x/v. Так что колебания любой точки среды описываются уравнением
x=Acosw 
. (31.2)
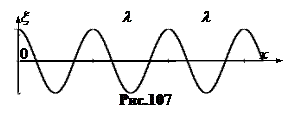
Это уравнение плоской гармонической монохроматической волны, которая распространяется в среде без затухания. Минимальное расстояние между однофазными волновыми поверхностями называют длиной волны l, а их скорость перемещения называют фазовой скоростью v. (рис.107) Фазовая скорость, длина волны и частота колебания частиц связаны между собой: v =ln. (31.3)
|
|
|
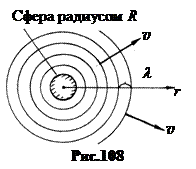
б. Сферическая волна генерируется шаровым телом или сферической поверхностью (рис.108). Уравнение сферической волны в среде без затухания имеет вид:
x=A0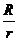 
cosw 
, r >> R. (31.4)
Убывание амплитуды по мере удаления волны от центра объясняется возрастанием волновой поверхности с ростом r, в результате энергия волнового движения распределяется на все большее число частиц.
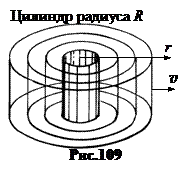
в. Цилиндрическая волна (рис.109) генерируется боковой поверхностью длинного цилиндра. Уравнение цилиндрической волны в среде без затухания имеет вид:
x =A0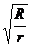 
cosw . (31.5)
3. Продольные и поперечные волны. В зависимости от направления смещения частиц среды упругие волны бывают продольными и поперечными.
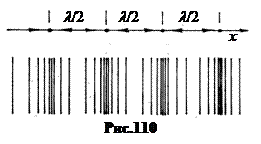а. В продольной волне частицы среды колеблются вдоль направления распространения волны (рис.110). Это так называемые волны сжатия. Продольные волны могут распространяться в твердых, жидких и газообразных телах. Скорость распространения продольной волны 
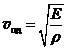, (31.6)
|
|
|
где Е – модуль Юнга, если волна распространяется в твердом теле, или модуль всестороннего сжатия, если волна распространяется в жидкости или в газе, r – плотность среды.
б. В поперечной волне частицы отклоняются от положения равновесия в направлении, перпендикулярном направлению распространения волны (рис.111). Скорость поперечной волны определяется формулой: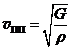 
. (31.7)
Здесь G – модуль сдвига среды, r – плотность среды.
Поперечные волны могут существовать только в твердых упругих телах.
4. Стоячие волны. Если волна распространяется в ограниченном пространстве, то могут возникать ситуации, когда из бегущей волны формируется стоячая волна (рис.112).
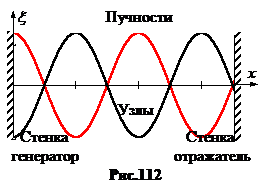Для появления стоячих волн нужно, чтобы бегущая волна отражалась от границы среды без затухания и чтобы на отрезке между стенкой-генератором и стенкой-отражателем укладывалось целое число полуволн, l =N 
. (N=1, 2, 3, ..) (31.8)
Координаты пучностей хпучн = n , (n=0, 1, 2, ..)(31.9)
Координаты узлов хузлов=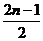 
× , (n=1,2,3,..) (31.10)
Немецкий физик Эрнст Хладни (I756–I827) предложил в 1787 году метод наблюдения схемы расположения стоячих волн в упругих пластинках. Если на горизонтально расположенную пластинку насыпать песок и провести по ее краю смычком, то при колебаниях пластинки частицы песка соберутся в области узлов. На поверхности пластинки появляются так называемые фигуры Хладни (рис.113).
|
|
|
5. Энергия бегущей волны. Вектор Умова. Энергетический поток бегущей упругой волны нашел теоретическим путем в 1874г. русский физик Николай Умов (I846–I9I5). Средняя плотность потока энергии, т.е. количество энергии, переносимое бегущей волной через единичную площадку в единицу времени, определяется выражением:
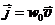. Вектор Умова, 1874 (31.11)
Здесь w0 – средняя плотность энергии волны, v – скорость.
Если вместо средней плотности энергии использовать мгновенную плотность энергии, то формула вектора Умова будет выражать мгновенную плотность потока энергии.
Найдем зависимость среднего значения вектора Умова от параметров волны.
Величина w0 определяет механическую энергию единицы объема среды. Как известно, механическая энергия гармонического осциллятора составляет E = mA2 
. Применительно к единице объема среды m=r, и средняя плотность энергии w0 =rA2 . Отсюда среднее значение плотности потока энергии бегущей волны равно
|
|
|
= 
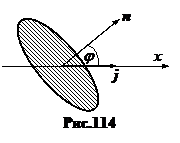
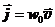. (31.12)
Количество энергии, переносимое бегущей волной через поверхность S в единицу времени, есть поток энергии (рис.114)
F = jScos( 
^ 
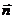) = jnS. (31.13)
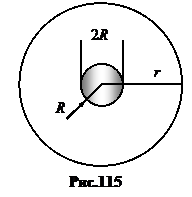Здесь n – единичный вектор нормали к площадке. В качестве примера найдем, как изменяется амплитуда колебания частиц среды в сферических и цилиндрических волнах.
Пример 31.1. Сферическая волна. Поскольку среда без затухания, то поток энергии через любую сферу, охватывающую излучатель, равна потоку энергии от излучателя:
F = jS = 
.
Здесь A0 – амплитуда колебаний поверхности сферы-генератора, А – амплитуда колебания частиц среды, R – радиус сферы-генератора (рис.115). Отсюда
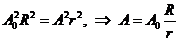. (31.14)
Пример 31.2. Цилиндрическая волна. Если излучающий цилиндр достаточно длинный, то можно считать, что вся энергия волны распространяется в радиальных направлениях. Тогда F = jS = 
. (31.15)
Здесь R – радиус цилиндра-генератора, h – его высота (длина).
6. Затухающие волны. Если среда вязкая, то механическая энергия упругой волны постепенно рассеивается, то есть превращается в тепло. Амплитуда плоской волны уменьшается с расстоянием до стенки-излучателя (рис.116).
Уравнение плоской бегущей волны в вязкой среде имеет вид: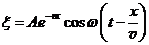 
. (31.16)
Здесь n – коэффициент затухания волны.
Определим расстояние l, на котором амплитуда колебания частиц среды уменьшается в е раз. Полагаем затухание слабым, так что l >> l. Поэтому без большой погрешности можно принять, что на отрезке l укладывается целое число волн, l = Nl. Это позволяет сравнивать амплитуды частиц, колеблющихся в одной фазе.
Запишем уравнение волны для частиц с координатами х и х + l.
, 
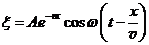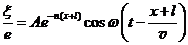. (31.17)
Разделим 1-е уравнение на 2-е. Так как частицы колеблются в одной фазе, то косинусы сокращаются. Получаем e = enl, Þ nl = 1, и n =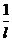 
. (31.18)
Итак, коэффициент затухания n есть величина, обратная отрезку, на котором амплитуда волны уменьшается в e раз.
Звуковые волны. Акустика
1. Природа звука. Звук – явление, воспринимаемое специальным органом чувств человека и животных. Звуковые волны в воздухе представляют собой продольные механические волны. Они испускаются источником звука – колеблющимся телом – и распространяются в твердых телах, жидкостях и газах в виде колебаний давления.
Обычное человеческое ухо воспринимает звуковые колебания в диапазоне частот от 16 до 20 000 Гц. Поскольку звуковые волны – это обычные волны упругости, то к ним применима вся теория упругих волн. Но поскольку волны указанного диапазона имеют большое значение в жизни людей, то теория звуковых волн выделилась исторически в особый раздел – акустику (от греческого akustikos – слуховой).
Упругие колебания частотой более 20 000 Гц называют ультразвуком, а частотой менее 16 Гц – инфразвуком.
2. Источники звука. Это колеблющиеся тела, возбуждающие в среде звуковые волны. Они могут быть твердыми (струна, стержень, пластина), газообразными (струя реактивного двигателя, столб воздуха) и жидкими (водопад). Рассмотрим примеры:
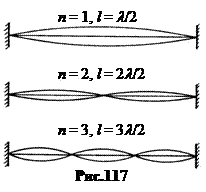а. Струна с закрепленными концами(рис.117). Частота основного тона свободно колеблющейся струны определяется формулой: 
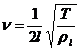, (32.1)
где l – длина струны, Т – сила ее натяжения, rl – линейная плотность струны (масса единицы длины).
Кроме основного тона, когда на струне возникает стоячая полуволна, l =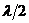 
, струна может излучать и более высокие тоны (обертоны), когда на струне возникает 2, 3, 4 и т.д., то есть любое целое число стоячих полуволн. Общая формула собственных частот колебаний струны: 
. (32.2)
Число n показывает количество стоячих полуволн на струне.
б. Камертон. Представляет собой стальной стержень, изогнутый в виде латинской буквы U (рис.118). Середина стержня закрепляется неподвижно, а концы остаются свободными и могут колебаться. Поскольку собственная частота колебаний камертонов очень слабо зависит от внешних воздействий, то их используют, в основном, в качестве эталонных источников звука. Чаще всего камертоны настраивают на частоту 440 Гц.
в. Звучащие пластины используются в литаврах, ксилофонах, металлофонах.
г. Столб воздуха звучит в духовых музыкальных инструментах, органных трубах, свистках.
3. Скорость звука в газах. Распространение звука в газах – адиабатный процесс (теплопроводность не играет роли), для которого модуль всестороннего сжатия E = gp. Здесь g – показатель адиабаты. Для двухатомных газов, в том числе и для воздуха, g = 1,4. Для одноатомных газов g =1,66 (гелий, неон, пары металлов), для многоатомных газов g =1,33 (углекислый газ, пары воды, метан и др. углеводороды). Формула скорости звука в газах имеет вид: 
. (32.3)
Если давление p выразить из уравнения Клапейрона-Менделеева, то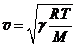 
(32.4)
Здесь R = 8,31 Дж/(К×моль) – универсальная газовая постоянная, М – молярная масса газа, Т – его абсолютная температура. При Т = 273 К скорость звука в воздухе составляет 332 м/с.
4. Характеристики звука. Поскольку звук – объективный волновой процесс, то к нему применимы все характеристики упругих волн. Наряду с кинематическими – скоростью, частотой, фазой, длиной волны – звук характеризуется и энергетическими величинами – интенсивностью и звуковым давлением.
а. Интенсивность звука – это средняя плотность потока энергии, иначе, это среднее по времени значение вектора Умова. I=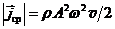 
. (32.5)
Единица измерения I в СИ – Вт/м2. Принято считать стандартным порогом слышимости человеческого уха интенсивность I0 = 1 пиковатт/м2. Интенсивность 10 Вт/м2 вызывает боль в ушах и называется порогом болевого ощущения.
б. Среднее звуковое давление – это среднее по времени среднеквадратичное избыточное давление в газе, обусловленное волновым процессом. Между средним звуковым давлением и интенсивностью звука существует связь: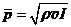 
. (32.6)
Стандартное пороговое звуковое давление составляет 2×10–5 Па, порог болевого ощущения по среднему звуковому давлению составляет @100 Па. (Все данные для частоты 1000 Гц).
в. Уровень интенсивности L, есть логарифм десятичный отношения интенсивности звука I к стандартному порогу слышимости I0, то есть L=lg( 
). (32.7)
Единица измерения уровня интенсивности – бел (Б). Это безразмерная величина, названа так в честь изобретателя телефона шотландца (по рождению) Александра Белла (I847–I922). Белл – очень крупная единица, весь диапазон уровней интенсивности, воспринимаемых человеческим ухом, составляет всего 13 бел. Поэтому на практике используют величину в 10 раз меньшую – децибел, 1 дБ = 0,1 Б. Выражение для L в децибелах принимает вид: L=10×lg( ) дБ. (32.8)
| Излучатель звука | Интенсивность звука, Вт/м2 | Среднее звуковое давление, Па | Уровень интенсивности, дБ |
| Порог слышимости Тиканье часов Разговор Крик Кузнечный цех Самолетный двиг.4 м Болевой порог | 10–12 10–11 10–7 10–4 10–2 1 10 | 2×10–5 6×10–5 6×10–3 2×10–1 2 20 60 | 0 10 50 80 100 120 130 |
5. Субъективные характеристики звука применяются для описания музыкальных звуков. Важнейшими из них являются высота тона и тембр.
а. Высота тона звука соответствует частоте колебаний частиц в звуковой волне n. Чем больше n, тем выше тон, и наоборот. Высота тона в музыке описывается нотами. В России принята частотная шкала нот, введенная Международным конгрессом в 1939г.
Приведем в качестве примера частоты, соответствующие нотам первой октавы.
до ре ми фа соль ля си
261,6 293,7 329,6 349,2 392,0 440,0 493,9
Обычно любой стандарт задает лишь значение частоты одной ноты. В данном случае это нота Ля, ее частота принята равной 440 Гц точно. Все остальные ноты "получают" свои частоты с помощью определенных соотношений.
б. Тембр, иначе, окраска звука. Различают чистый тон, музыкальные звуки и шумы.
Чистый тон соответствует звуковой волне, частицы среды в которой колеблются строго по гармоническому закону (рис.119-a).
Музыкальный звук есть сумма нескольких чистых тонов различных интенсивностей (рис.119-б). Тон самой низкой частоты определяет общую высоту звука, более высокие тоны (обертоны) определяют окраску звука, или, иначе, тембр. Частицы среды в музыкальном звуке совершают сложные периодические колебания.
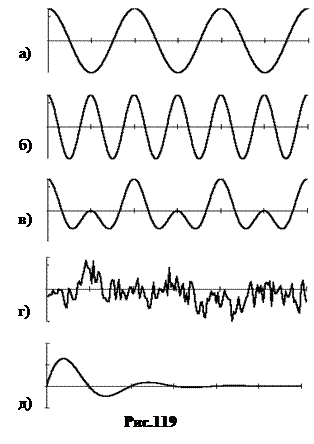Шум – немузыкальный звук. Частицы среды при шуме совершают непериодические колебания (рис.119-в и 119-г).
в. Громкость подобно уровню интенсивности определяется логарифмом отношения звукового давления к стандартному пороговому звуковому давлению. Если сравнить логарифм отношения давлений с логарифмом отношения интенсивностей, то оказывается, что:
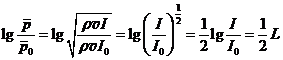. (32.9)
Это значит, что 13 белам уровня интенсивности слышимого диапазона соответствует в два раза меньшее количество единиц громкости, т.е. 13/2 = 6,5. Чтобы привести в соответствие число единиц уровня интенсивности (число децибел) с числом единиц громкости, громкость определяют выражением: 
. (32.10)
В этом случае шкала громкости практически совпадает со шкалой уровня интенсивности. Единица громкости – фон – равняется децибелу. Поэтому громкость определяют часто как уровень интенсивности и выражают в децибелах.
6. Спектральный анализ звука. Как уже говорилось, любой музыкальный звук есть сумма чистых тонов. Поэтому можно поставить задачу: определить, из каких чистых тонов состоит данный звук. Эта задача решается в рамках спектрального анализа звука. Есть два пути – теоретический и практический.
В основе теоретического метода лежит теорема, сформулированная в 1822г. французским ученым Жаном Фурье (I768–I830) и утверждающая, что любую сложную периодическую функцию можно представить как сумму простых гармонических. Зная кинематический закон сложного периодического движения частиц среды в звуковой волне с помощью математических методов можно определить частоты простых тонов и соответствующие им амплитуды.
Практический путь состоит в том, что изготовляются устройства, в каждом из которых звук возбуждает чистый тон определенной частоты. Если имеется набор таких устройств (их называют резонаторами) с разными частотами собственных тонов, то процедура анализа сводится к выяснению: в которых резонаторах возбуждается звук и какой громкости. По номеру резонатора определяется частота чистого тона, а по громкости – соответствующая этому тону амплитуда колебания частиц.
На графике спектр звука представляют обычно в декартовых координатах, где по оси абсцисс откладывается частота простых тонов, а по оси ординат – их амплитуда (рис.120).
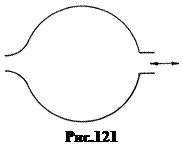
Примером устройств для спектрального анализа звука являются акустические резонаторы Геймгольца (рис.121).
Акустический эффект Доплера
1.Эффект Доплерасостоит в том, воспринимаемая наблюдателем частота звука n при относительном сближении наблюдателя с источником звука повышается по сравнению с генерируемой источником частотой n0, а при относительном удалении – понижается.
Теоретически объяснил это явление Христиан Доплер в 1842 году. Рассмотрим подробнее несколько случаев.
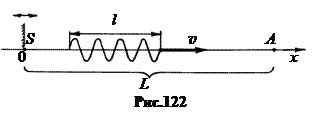2.Источник звука и наблюдатель покоятся относительно друг друга и среды. Пусть наблюдатель А находится относительно источника звука S на расстоянии L (рис.122). В течение некоторого времени t источник S колебался с частотой n0. Вопрос: какой частоты звук будет воспринимать наблюдатель А?
Излученный источником S за конечное время t звуковой импульс можно рассматривать как отрезок синусоиды длиной l = vt, где v - скорость звука в среде. В этом отрезке l помещается N =n0 ·t колебаний. Длина волны в среде
l0 = l/N = v·tçn0·t = vçn0. (33.1)
Поскольку все точки синусоиды движутся относительно среды с одинаковой скоростью v, то, спустя время lçv, волновой импульс длиной l пройдет мимо наблюдателя А в течение времени t=lçv. За это время наблюдатель А воспримет в звуковой волне N колебаний частотой n = 
. (33.2)
Итак, если источник звука S и наблюдатель А неподвижны друг относительно друга и относительно среды, то наблюдатель воспринимает звук той же частоты n0, какой он генерируется источником.
Дата добавления: 2018-04-15; просмотров: 676; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!