Задания для самостоятельного решения.
1.Решите систему линейных уравнений с помощью обратной матрицы:
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
7) 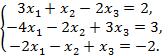 8)
8) 
9)  10)
10) 
2. Решите систему линейных уравнений, используя правило Крамера:
1)  2)
2) 
3)  4)
4) 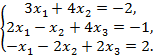
5) 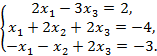 6)
6) 
7)  8)
8) 
9)  10)
10) 
3. Решите систему линейных уравнений методом Гаусса:
1) 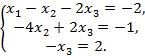 2)
2) 
3)  4)
4) 
5) 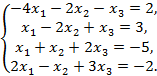 6)
6) 
7)  8)
8) 
9) 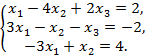 10)
10) 
4. Решите однородную систему линейных уравнений, выделив какую-либо фундаментальную систему:
1)  2)
2) 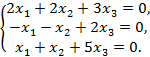
3)  4)
4) 
5)  6)
6) 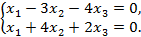
7)  8)
8) 
9)  10)
10) 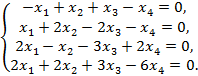
Дифференциальное исчисление
Пределы
Число А называется пределом функции f(x) при  , если для любого сколь угодно малого
, если для любого сколь угодно малого  найдется такое значение
найдется такое значение  , что при
, что при  . Пишут
. Пишут 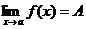 . Практическое вычисление пределов основывается на следующих теоремах:
. Практическое вычисление пределов основывается на следующих теоремах:
Если существуют конечные пределы  и
и  , то
, то
1)  , (1)
, (1)
2) 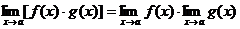 , (2)
, (2)
3)  (при
(при  ) (3)
) (3)
Используя также следующие пределы:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 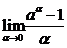 ;
;
5)  . (4)
. (4)
Здесь  - бесконечно малая функция
- бесконечно малая функция 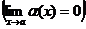
Сравнение бесконечно малых
Пусть  и
и  бесконечно малые при
бесконечно малые при  . Если
. Если  , то бесконечно малые называются эквивалентными. Пишут: α~β.
, то бесконечно малые называются эквивалентными. Пишут: α~β.
|
|
|
Теорема. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой, то есть если  α~
α~  , β~
, β~  , то
, то
 (5)
(5)
Полезно использовать эквивалентность следующих бесконечно малых: если  , то
, то
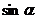 ~α, tgα~α, arcsinα~α, arctgα~α, ln(1-α)~α,
~α, tgα~α, arcsinα~α, arctgα~α, ln(1-α)~α,
 ~αln
~αln  ,
,  ~αm (5’)
~αm (5’)
Дифференцирование функций
Производной от функции  в точке х называется конечный предел
в точке х называется конечный предел 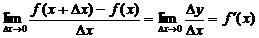 (6)
(6)
Нахождение производной называется дифференцированием функции.
Основные правила дифференцирования
Пусть С=const, u=u(x), v=v(x) – дифференцируемые функции. Тогда:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 
если  , то
, то  (7)
(7)
Производная степенно – показательной функции
 , (8)
, (8)
где u=u(x), v=v(x) – дифференцируемые функции.
Таблица производных
1.  , С - любое число 10.
, С - любое число 10. 
2. 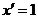 11.
11. 
3.  12.
12. 
4.  13.
13. 
5.  14.
14. 
6.  15.
15. 
|
|
|
7.  16.
16. 
8. 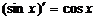 17.
17. 

9. 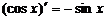 18.
18. 
Интегральное исчисление
Неопределенный интеграл. Его свойства
Функция 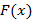 называется первообразной для функции
называется первообразной для функции 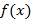 в промежутке
в промежутке  , если в любой точке этого промежутка ее производная равна
, если в любой точке этого промежутка ее производная равна 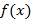 :
:

Интегрирование – это процесс нахождения первообразных.
Множество первообразных для данной функции f(x) называется неопределенным интегралом и обозначается 
Примеры:


Таблица неопределенных интегралов
1.  .
.
2.  .
.
3. 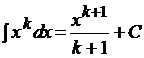
 .
.
4.  .
.
5. 
 .
.
6.  .
.
7. 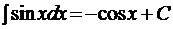 .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12. 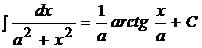 .
.
13.  .
.
14. 
Свойства неопределенного интеграла:
1. Если  – постоянная величина, то
– постоянная величина, то  .
.
2. 
3.  .
.
4.  .
.
5.  .
.
Определенный интеграл
Разность  называется определенным интегралом от функции f(x) и обозначается
называется определенным интегралом от функции f(x) и обозначается  , где
, где 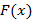 первообразная для функции
первообразная для функции 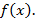
 - формула Ньютона – Лейбница.
- формула Ньютона – Лейбница.
Пример.

Свойства определенного интеграла аналогичны свойствам неопределенного интеграла.
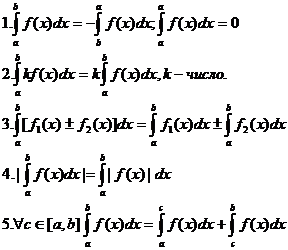
Дифференциальные уравнения
Основные понятия и определения
Дифференциальным уравнением называется уравнение, связывающее независимую переменную  , искомую функцию
, искомую функцию 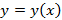 и производные этой функции, т.е. уравнение вида
и производные этой функции, т.е. уравнение вида 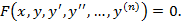
|
|
|
Если искомая функция 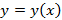 есть функция одной переменной
есть функция одной переменной  , то дифференциальное уравнение называется обыкновенным.
, то дифференциальное уравнение называется обыкновенным.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Например,
1.  – обыкновенное дифференциальное уравнение первого порядка.
– обыкновенное дифференциальное уравнение первого порядка.
2.  – дифференциальное уравнение второго порядка.
– дифференциальное уравнение второго порядка.
Обыкновенное дифференциальное уравнение первого порядка имеет вид 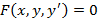 или
или 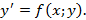 Решением дифференциального уравнения на интервале
Решением дифференциального уравнения на интервале  называется функция
называется функция  , определенная на интервале
, определенная на интервале  вместе со своими производными, и такая, что подстановка функции
вместе со своими производными, и такая, что подстановка функции  в дифференциальное уравнение превращает последнее в тождество по
в дифференциальное уравнение превращает последнее в тождество по  на
на 
Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Общим решением дифференциального уравнения  в области
в области  называется функция
называется функция  , обладающая следующими свойствами:
, обладающая следующими свойствами:
1) эта функция является решением дифференциального уравнения при любом значении произвольной постоянной  , принадлежащей некоторому множеству;
, принадлежащей некоторому множеству;
|
|
|
2) для любого начального условия  такого, что
такого, что  , существует единственное
, существует единственное  , при котором решение удовлетворяет заданному начальному условию.
, при котором решение удовлетворяет заданному начальному условию.
Частным решением дифференциального уравнения  называется такое решение
называется такое решение  , которое получается из общего решения
, которое получается из общего решения  при некотором частном значении произвольной постоянной
при некотором частном значении произвольной постоянной  .
.
Задача Коши для дифференциального уравнения первого порядка  состоит в том, чтобы найти решение, которое при заданном значении аргумента
состоит в том, чтобы найти решение, которое при заданном значении аргумента  принимает заданное значение
принимает заданное значение 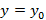 , т.е. удовлетворяет начальному условию
, т.е. удовлетворяет начальному условию  Другими словами, задача Коши состоит в нахождении частного решения.
Другими словами, задача Коши состоит в нахождении частного решения.
Геометрически задача Коши формулируется следующим образом: среди всех интегральных кривых данного дифференциального уравнения выделить ту, которая проходит через заданную точку 
Дата добавления: 2018-04-15; просмотров: 421; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
