Метод Гаусса для исследования и решения СЛАУ
Матричный метод и правило Крамера обладают двумя существенными недостатками. Во–первых, они применимы только для систем с невырожденной квадратной матрицей и не работают в случае, когда 
. Во–вторых, с ростом 
объём вычислений для этих методов слишком быстро возрастает и для 
они уже практически неприменимы. Для исследования систем линейных уравнений и нахождения их решений можно использовать метод Гаусса.
Исследовать систему – это значит определить совместна ли она и, в случае совместности, определить, сколько решений она имеет.
Расширенной матрицей СЛАУ. называется матрица, полученная из матрицы системы приписыванием справа столбца свободных членов системы.
Для системы из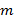 
уравнений с неизвестными, она имеет размер 
и обозначается через 
.
Свободные члены обычно отделяются вертикальной чертой.
Понятно, что ранг либо равен рангу 
, либо превышает его на 
. Следующая теорема позволяет устанавливать факт совместности или несовместности системы.
Теорема Кронекера – Капелли. Система линейных алгебраических уравнений совместна только в том случае, когда ранг её матрицы совпадает с рангом расширенной матрицы 
Если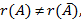 
то СЛАУ решений не имеет.
Для совместных систем линейных уравнений верны следующие теоремы.
1) Если ранг матрицы совместной системы равен числу неизвестных, т.е. 
, то система имеет единственное решение.
2) Если ранг матрицы совместной системы меньше числа неизвестных, т.е 
, то система неопределенная и имеет бесконечное множество решений.
|
|
|
Пусть 
и 
- неизвестных 
называются базисными, если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные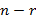 
называются свободными.
При решении системы линейных уравнений не нужно отдельно вычислять ранги, а затем их сравнивать. Достаточно сразу применить метод Гаусса.
Преобразования Гаусса удобно проводить, осуществляя преобразования не над самими уравнениями, а над матрицей их коэффициентов.
Достоинства метода Гаусса по сравнению с другими:
1) Значительно менее трудоемкий.
2) Позволяет однозначно установить, совместна система или нет, а в случае совместности найти её решения (единственное или бесконечное множество).
3) Дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.
Однородные и неоднородные системы линейных алгебраических уравнений
Система ЛАУ, все свободные члены которой нулевые, называется однородной.
СистемаЛАУ, столбец свободных членов которой ненулевой, называется неоднородной.
В общем случае однородная система из m уравнений с n неизвестными имеет вид:
|
|
|
В матричной форме она записывается в виде 
Здесь
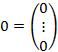
нулевой столбец.
Однородная система всегда совместна, так как она имеет решение 
, которое называется тривиальным. Матричный метод и метод Крамера не имеет смысла применять для решения однородных систем с квадратной матрицей . Поскольку, если не вырождена, то система имеет единственное тривиальной решение, если же 
, то эти методы неприменимы, система имеет бесконечное число решений.
Метод Гаусса для решения однородных систем используется в следующем виде.
Записываем матрицу системы и с помощью элементарных преобразований приводим её к треугольному виду. Возможны два случая.
1) 
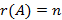. Система имеет единственное тривиальное решение.
2) 
Система имеет бесконечно много решений, зависящих от 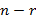параметров.
Обозначим решение системы 
в виде строки 
Решения системы линейных однородных уравнений обладают следующими свойствами.
1)Если строка - решение системы 
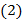, то и строка 
- также решение этой системы.
2)Если строка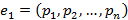 
и 
- решения системы , то при любых 
их линейная комбинация 
- также решение данной системы.
Набор строк (решении системы ) 
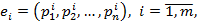называется линейно зависимым, если существуют одновременно не равные нулю числа 
такие, что выполняется равенство:
|
|
|
Если равенство 
выполняется только при 
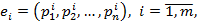, то набор решении называется линейно независимым.
Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы.Поэтому представляет интерес найти такие линейно независимые решения системы 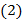, через которые линейно выражались бы все остальные ее решения.
Система линейно независимых решений 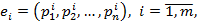называется фундаментальной, если каждое решение системы 
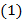является линейной комбинацией решений 
.
Теорема. Если ранг матрицы коэффициентов при неизвестных системы линейных однородных уравнений 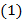меньше числа неизвестных , то всякая фундаментальная система решений системы 
) состоит из 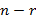решений. Поэтому общее решение системы 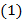линейных однородных уравнений имеет вид: 
, где 
- любая фундаметальная система решений, - произвольные числа и 
Примеры.
1.Решим систему
матричным методом.
Решение.Матрица этой системы
невырожденная,т. к. 
.
Найдём обратную матрицу
Для данной системы
,
Поэтому
,
Следовательно
2. Решим систему
по правилу Крамера.
поэтому:
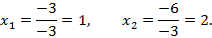
3. Исследовать и решить систему
|
|
|
Запишем расширенную матрицу 
и приведём её к треугольному виду:
т.к. 
система совместна и имеет единственное решение. По последней матрице восстанавливаем систему и решаем её, начиная с последнего уравнения.
4. Исследовать и решить систему
Запишем и приведем к треугольному виду матрицу .
Мы получили, что 
Система решений не имеет.
5. Исследовать и решить систему
Запишем и приведем к треугольному виду матрицу .
Здесь 
. Система имеет бесконечно много решений зависящих от 3–2=1 свободного неизвестного 
. Задавая свободному неизвестному произвольные значения 
, найдем бесконечное множество решений системы. Восстановим систему по последней матрице и решим её.
6. Решите систему уравнений
Запишем матрицу системы и преобразуем её.
, следовательно, система имеет единственное решение: 
7).Решите систему уравнений
Преобразуем матрицу системы.
, поэтому система имеет бесконечно много решений, зависящих от одного параметра.
Восстановим систему и решим её.
Найдем фундаментальную систему решений. Решения данной системы должны удовлетворять двум уравнениям: 
Общее решение системы будет иметь вид:
Получили, что всякое решение исходной системы является линейной комбинацией решения 
т.е. решение 
является фундаментальной системой решения исходной системы, т.е.
Дата добавления: 2018-04-15; просмотров: 656; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!