Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

где постоянные 
Найдем общее решение такого уравнения.
Будем искать частное решение уравнения 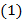 в форме
в форме  , где k -постоянное число, подлежащее определению.
, где k -постоянное число, подлежащее определению.
Имеем: 
Следовательно, должно иметь место тождество

или, так как  то
то 
Уравнение

называется характеристическим уравнением для уравнения 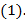
В зависимости от корней  характеристического уравнения
характеристического уравнения 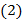 получаем общее решение уравнения (1) в виде
получаем общее решение уравнения (1) в виде

если  - различные действительные числа;
- различные действительные числа;

если  ;
;

если  - комплексные числа,
- комплексные числа,  – произвольные постоянные.
– произвольные постоянные.
Рассмотрим дифференциальное уравнение третьего порядка:

Характеристическое уравнение

Если корни действительные и  , то общее решение имеет вид:
, то общее решение имеет вид:

Если корни действительные и  , то общее решение имеет вид:
, то общее решение имеет вид:

Если корни действительные и  , то общее решение имеет вид:
, то общее решение имеет вид:

Если корни действительные и  , то общее решение имеет вид:
, то общее решение имеет вид:

Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Рассмотрим линейное уравнение

1. Пусть правая часть уравнения  имеет вид
имеет вид

где  многочлен. Тогда уравнение
многочлен. Тогда уравнение  имеет частное решение вида
имеет частное решение вида

где  -многочлен той же степени, что и
-многочлен той же степени, что и  , причем если число
, причем если число 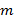 не является корнем характеристического уравнения
не является корнем характеристического уравнения  , то
, то  , а если является, то
, а если является, то  -кратность этого корня.
-кратность этого корня.
2. Пусть правая часть уравнения  имеет вид
имеет вид
|
|
|

Если числа  не являются корнями характеристического уравнения, то уравнение имеет частное решение вида
не являются корнями характеристического уравнения, то уравнение имеет частное решение вида 
Если же числа  служат корнями характеристического уравнения, то частное решение имеет вид
служат корнями характеристического уравнения, то частное решение имеет вид 
3. Если правая часть уравнения  имеет вид
имеет вид

где 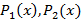 -многочлены, а числа
-многочлены, а числа  не являютсякорнями характеристического уравнения, то частное решение следует искать в виде
не являютсякорнями характеристического уравнения, то частное решение следует искать в виде

где 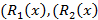 -многочлены степени, равной высшей из степеней многочленов
-многочлены степени, равной высшей из степеней многочленов 
Если числа  являются корнями характеристического уравнения, то частное решение следует искать в виде
являются корнями характеристического уравнения, то частное решение следует искать в виде

4. Если правая часть  уравнения
уравнения  равна сумме функций
равна сумме функций

и 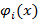 - частные решения уравнений
- частные решения уравнений
 соответственно, то сумма
соответственно, то сумма
 есть частное решение уравнения
есть частное решение уравнения  .
.
Примеры.
1.Найти общее решение уравнения

Решение.


Отсюда имеем

Предположим, что  . Разделим на
. Разделим на  .
.

Интегрируя, будем иметь

или

Потенцируя последнее равенство, окончательно получим  .
.
2. Проинтегрировать дифференциальное уравнение. 
Найти частное решение, удовлетворяющее условию:  при
при 
Решение. Данное уравнение является уравнением с разделяющимися переменными. Разделив обе части уравнения на произведение 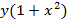 , получим уравнение
, получим уравнение
|
|
|

Интегрируем.



Откуда получаем общее решение

Чтобы найти искомое частное решение, достаточно определить значение произвольной постоянной по начальным условиям.
 .
.
Следовательно, частное решение имеет вид

3. Найти общее решение уравнения.

Решение.Разделим данное уравнение относительно производной  :
:
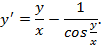
Правая часть уравнения зависит от отношения  , следовательно, данное уравнение является однородным.
, следовательно, данное уравнение является однородным.
Введем новую функцию  :
:

Тогда 
Подставляем полученное выражение в уравнение, получим уравнение с разделяющимися переменными

или

Разделим переменные и проинтегрируем
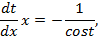



Подставив вместо  его значение, получим общий интеграл.
его значение, получим общий интеграл.

4. Решить дифференциальное уравнение

Решение. Решим уравнение относительно производной 



Правая часть уравнения зависит от отношения

следовательно, данное уравнение является однородным.
Введем новую функцию  :
:

Тогда  Подставляем полученное выражение в уравнение:
Подставляем полученное выражение в уравнение:










и, следовательно,


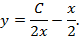
5. Найти общее решение линейного уравнения 
Решение. Положим  , тогда
, тогда 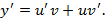



Выберем  так, чтобы выражение в скобках обратилось в нуль, тогда
так, чтобы выражение в скобках обратилось в нуль, тогда
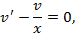

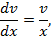

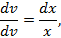

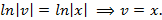







Следовательно, 
6. Найти частное решение уравнения 
|
|
|
Решение.






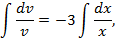




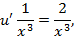
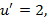



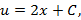





6. Решить уравнение

Решение.Полагая  приходим к уравнению первого порядка
приходим к уравнению первого порядка

Уравнение является линейным.
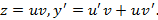
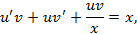













Тогда


7. Решить уравнение

Решение.
Полагая

получим:

Это уравнение первого порядка с разделяющимися переменными.








8. Найти общее решение уравнения

Решение. Характеристическое уравнение для данного уравнения принимает вид

Т.к.  , то в соответствии с формулой
, то в соответствии с формулой  общее решение данногодифференциального уравнения имеет вид
общее решение данногодифференциального уравнения имеет вид
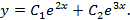
9. Найти общее решение уравнения

Решение. Характеристическое уравнение  имеет корни
имеет корни 
В соответствии с формулой  получаем общее решение исходного дифференциального уравнения
получаем общее решение исходного дифференциального уравнения

10.Проинтегрировать уравнение

Решение. Характеристическое уравнение 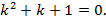 Найдем корни этого уравнения.
Найдем корни этого уравнения.




В соответствии с формулой  находим общее решение
находим общее решение

11. Найти частное решение дифференциального уравнения.

Решение. Характеристическое уравнение 

Т.к. корни  - различные действительные, то общее решение уравнения имеет вид
- различные действительные, то общее решение уравнения имеет вид
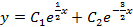
Найдем частное решение.
Подставим в общее решение первое начальное условие:

|
|
|
Чтобы составить второе уравнение, продифференцируем общее решение и воспользуемся вторым начальным условием:
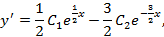

Решим систему уравнений:
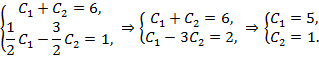
Подставив найденные значения постоянных в общее решение, получим частное решение

12. Найти общее решение уравнения

Решение. Составляем характеристическое уравнение
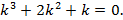
и находим его корни:

Следовательно, уравнение имеет три действительных корня, причем два из них равные.
Общее решение уравнения

Где  - произвольные постоянные.
- произвольные постоянные.
13.Решить уравнение

Решение.Cоставим характеристическое уравнение

Преобразуя левую часть уравнения, получим

Откуда 
Получаем общее решение уравнения
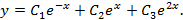
14Найти общее решение уравнения

Решение. Найдем общее решение уравнения

Характеристическое уравнение

имеет двукратный корень  1. Значит, общее решение однородного уравнения имеет вид
1. Значит, общее решение однородного уравнения имеет вид

Правая часть имеет рассматриваемую форму, причем  .
.
Так как число  не является корнем характеристического уравнения, то частное решение ищем в виде
не является корнем характеристического уравнения, то частное решение ищем в виде
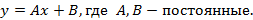
Дифференцируя и подставляя в дифференциальное уравнение, находим коэффициенты:

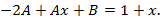
Приравнивая коэффициенты в обеих частях равенства

Получим
 .
.
Итак, частным решением заданного уравнения является функция

а его общим решением – функция

15. Найти общее решение дифференциального уравнения

Решение. Найдем общее решение однородного уравнения

Характеристическое уравнение 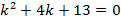 имеет корни
имеет корни 
Значит, общее решение соответствующего уравнения без правой части запишется так:
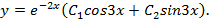
Так как числа  не являются корнями характеристического уравнения, то частное решение неоднородного уравнения ищем в виде
не являются корнями характеристического уравнения, то частное решение неоднородного уравнения ищем в виде

Дважды дифференцируем:
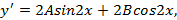

и подставляем в уравнение:
 Приравнивая друг другу коэффициенты при
Приравнивая друг другу коэффициенты при  в обеих частях равенства, получим:
в обеих частях равенства, получим:

Отсюда  т.е. частным решением будет функция
т.е. частным решением будет функция
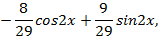
аобщим

16.Найти общее решение уравнения
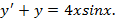
Решение. Найдем общее решение однородного уравнения

Характеристическое уравнение 
Корни характеристического уравнения 
Общее решение однородного уравнения имеет вид

Частное решение ищем в виде

Имеем:



Подставляя в уравнение, находим:
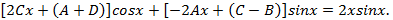
Это равенство будет тождественным только при
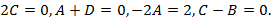
Отсюда  .
.
Следовательно, получаем частное решение

Общее решение имеет вид

Дата добавления: 2018-04-15; просмотров: 398; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
