Задачи для самостоятельного решения.
1.Найти частное решение.
1) 
2) 
3) 
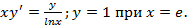
4) 
5) 
.
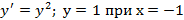6) 
2. Проинтегрировать дифференциальное уравнение с разделяющимися переменными.
1) 
2) 
3) 
4) 
5) 
6) 
3. Найдите общее решение однородного дифференциального уравнения.
1) 
2) 
3) 
4) 
5) 
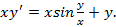
6) 
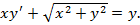
7) 
8) 
4. Решите линейное дифференциальное уравнение первого порядка.
1) 
2) 
3) 
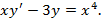
4) 
5) 
6) 
7) 
8) 
5. Найдите решение линейного дифференциального уравнения, удовлетворяющего заданному начальному условию.
1) 
2) 
3) 
4) 
5) 
6) 
7) 
6.Найдите общее решение дифференциального уравнения второго порядка с постоянными коэффициентами.
1) 
2) 
3) 
4) 
5) 
6) 
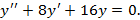
7) 
8) 
9) 
10) 
7. Решите задачу Коши для дифференциального уравнения второго порядка.
1) 
2) 
3) 
4) 
5) 
8. Решите линейное дифференциальное уравнение третьего порядка.
1) 
2) 
3) 
4) 
5) 
6) 
7) 
9. Решите линейное неоднородное дифференциальное уравнение.
1) 
2) 
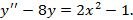
3) 
4) 
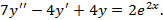
5) 
6) 
7) 
Комплексные числа
Комплексные числа и формы их записи
Комплексное число – это выражение вида:
где 
– действительная часть, обозначается 
; 
– мнимая часть, обозначается 
; 
– мнимая единица, такая, что:
Формула (1.1) называется алгебраической формой записи комплексного числа.
Комплексное число, как некоторую точку 
на комплексной плоскости, можно задать радиус-вектором 
и углом поворота 
этого вектора (рис.1).
Применяя формулы перехода из декартовой системы координат в полярную систему
|
|
|
получим комплексное число, записанное через тригонометрические функции, т.е. в тригонометрической форме:
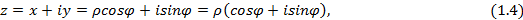
где - модуль комплексного числа 
- аргумент комплексного числа 
, где 
Формулы перехода от декартовых координат к полярным, задаются соотношениями:
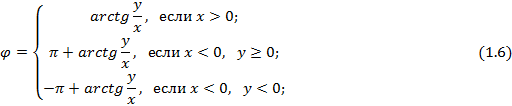
где 
Применяя к тригонометрической форме записи комплексного числа формулу Эйлера:
получим показательную или экспоненциальную форму записи комплексного числа:
Для каждого комплексного числа 
определено комплексно сопряженное число 
и определяемое формулами:
Важно знать, что
При вычислениях и доказательствах некоторых комплексных тождеств полезны следующие формулы:
Действия над комплексными числами, заданными в алгебраической форме
Сложение и вычитание
Действие сложения и вычитания комплексных чисел 
и 
производится по правилу сложения и вычитания двучленов
Умножение.
Действие умножение комплексных чисел и производится по правилу умножения двучленов
Деление.
Чтобы преобразовать дробь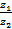 
в комплексное число, необходимо числитель и знаменатель дроби умножить на число сопряжённое к знаменателю, в числителе произвести действие умножения, а для знаменателя воспользоваться формулой (1.10)
|
|
|
Действия над комплексными числами, заданными в тригонометрической или в показательной форме
1. Умножение:
При умножении двух комплексных чисел, заданных в тригонометрической или показательной формах, их модули перемножаются, а аргументы складываются:
2. Деление:
При делении двух комплексных чисел, заданных в тригонометрической или показательной формах, их модули делятся, а аргументы вычитаются:
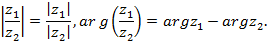
Возведение в степень.
Для возведения комплексного числа в целую положительную степень 
применяют формулу Муавра:
Данная формула является следствием формулы 
4. Извлечение корня порядка 
.
Для извлечения корня используем формулу:
где 
Точки, соответствующие 
являются вершинами правильного – угольника, вписанного в окружность с центром в начале координат и радиусом 
.
Способ построения для 
(рис.2):
1) Из начала координат описываем окружность радиуса 
.
 |
2) Если
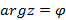то из начала координат проводим луч под углом 
к положительному направлению 
. Пересечение луча с окружностью дает точку 
.
3) Вписываем в окружность правильный – угольник, одна из вершин которого найденная точка . Точки пересечения – угольника и окружности есть решения 
|
|
|
Примеры.
1. Изобразить комплексные числа 
и 
на комплексной плоскости, если
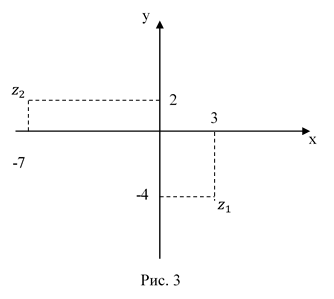
Решение.Для каждого комплексного числа выпишем действительную и мнимую части согласно формуле 
:
 |
На комплексной плоскости отметим две точки с соответствующими координатами:
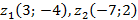(рис.3).
2. Возвести комплексное число в квадрат, если: 
Решение.Воспользуемся формулой сокращенного умножения 
, тогда 
Применяя формулу (1.2) к последнему слагаемому, окончательно получаем 
3. Найти аргумент комплексных чисел и ,если: 
Решение.Для нахождения аргумента комплексного числа воспользуемся формулой 
. Определим действительные и мнимые части заданных комплексных чисел:
Для числа : 
, следовательно
Для числа : 
, следовательно
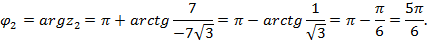
4.Выполнить действия 
, если известно, что: 
Решение. Рассматривая комплексные числа как двучлены выполним действия сложения, вычитания и умножения:
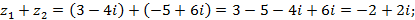
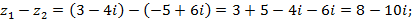
Найдем отношение
Умножим числитель и знаменатель дроби на число, сопряжённое к знаменателю 
Согласно формуле 
получим:
5. Перевести комплексное число 
в показательную форму и возвести в четвертую степень. Ответ записать в алгебраической форме.
Решение:Для того, перевести комплексное число в показательную форму, необходимо найти его модуль и аргумент . Для этого воспользуемся формулам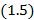и 
и . и определим действительную и мнимую части числа:
|
|
|
Получаем:
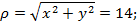
Тогда в показательной форме число имеет вид:
Возведём данное число в четвёртую степень используя формулу 
:
Учитывая, что функция 
имеет период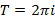 
, окончательно получаем:
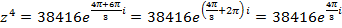
Для того, чтобы перевестичисло 
в алгебраическую форму определим и по формулам 
6.Найти модули комплексных чисел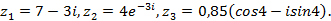 
и записать комплексно сопряжённые числа.
Решение:Число задано в алгебраической форме, для нахождения модуля воспользуемся формулой :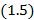 
следовательно,
Число задано в показательной форме 
, откуда следует, что 
Число 
задано в тригонометрической форме 
следовательно 
Определим комплексно сопряжённые числа по формулам (1.9). Получаем:
7. Для данного комплексного числа 
найти модуль.
Решение:Выражение представляет из себя произведение двух комплексных чисел 
и 
возведенных в степень. Для каждого из них вычислим модуль:
Согласно формуле Муавра , при возведении комплексного числа в степень, его модуль также возводится в данную степень, т.е.
При перемножении двух комплексных чисел. их модули перемножаются 
Следовательно,
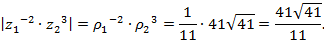
8. Вычислить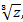 
если 
и изобразить найденные значения на комплексной плоскости.
Решение: Для вычисления 
переведём комплексное число в тригонометрическую форму, определив модуль и аргумент:
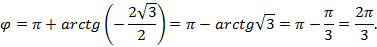
В тригонометрической форме получим:
Для извлечения корня порядка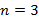 
воспользуемся формулой 
где 
Построим графическое представление корней:
1) Вычерчиваем окружность радиуса 
2) Откладываем угол
и на его пересечении с окружностью отмечаем корень .
3)
 |
Вписываем в окружность правильный треугольник (рис. 4).
9. Решить квадратное уравнение 
Решение: Решим данное квадратное уравнение через дискриминант:
Используя формулу 
, получим: 
Тогда
Или
Что подтверждает теорему о том, что если многочлен имеет комплексный корень, то он имеет и комплексно сопряженный корень.
Дата добавления: 2018-04-15; просмотров: 384; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!