Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца
Дальнейшие свойства связаны с понятиями минора и алгебраического дополнения
Минором элемента 
называется определитель, составленный из элементов, оставшихся после вычеркивания 
стоки и 
столбца, на пересечении которых находится этот элемент. Минор элемента определителя 
порядка имеет порядок 
. Будем его обозначать через 
.
Пример 1. Пусть 
, тогда 
.
Этот минор получается из A путём вычёркивания второй строки и третьего столбца.
Алгебраическим дополнением элемента называется соответствующий минор, умноженный на 
, т.е 
, где 
–номер строки и 
-столбца, на пересечении которых находится данный элемент.
VІІІ. (Разложение определителя по элементам некоторой строки). Определитель равен сумме произведений элементов некоторой строки на соответствующие им алгебраические дополнения.
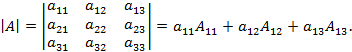
Пример 2.Пусть 
, тогда
Пример 3.Найдём определитель матрицы , разложив его по элементам первой строки.
Формально эта теорема и другие свойства определителей применимы пока только для определителей матриц не выше третьего порядка, поскольку другие определители мы не рассматривали. Следующее определение позволит распространить эти свойства на определители любого порядка.
Определителемматрицы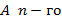 
порядка называется число, вычисленное с помощью последовательного применения теоремы о разложении и других свойств определителей.
Можно проверить, что результат вычислений не зависит от того, в какой последовательности и для каких строк и столбцов применяются вышеуказанные свойства. Определитель с помощью этого определения находится однозначно.
|
|
|
Хотя данное определение и не содержит явной формулы для нахождения определителя, оно позволяет находить его путём сведения к определителям матриц меньшего порядка. Такие определения называют рекуррентными.
Пример 4.Вычислить определитель: 
Хотя теорему о разложении можно применять к любой строке или столбцу данной матрицы, меньше вычислений получится при разложении по столбцу, содержащему как можно больше нулей.
Поскольку у матрицы 
нет нулевых элементов, то получим их с помощью свойства VII. Умножим первую строку последовательно на числа 
и прибавим её ко 
строкам и получим:
Разложим получившийся определитель по первому столбцу и получим:
=
так как определитель содержит два пропорциональных столбца.
Некоторые виды матриц и их определители
Квадратная матрица, у которой ниже или выше главной диагонали стоят нулевые элементы ( 
)называется треугольной.
Их схематичное строение соответственно имеет вид: 
или
.
Здесь 
– означает нулевые элементы, а 
– произвольные элементы.
|
|
|
Теорема. Определитель квадратной треугольной матрицы равен произведению её элементов, стоящих на главной диагонали, т.е.
.
Например,
Квадратная матрица, у которой вне главной диагонали стоят нулевые элементы, называется диагональной.
Её схематический вид
Диагональная матрица, у которой на главной диагонали стоят только единичные элементы, называется единичной матрицей. Она обозначается через:
Определитель единичной матрицы равен 
, т.е. 
Дата добавления: 2018-04-15; просмотров: 5021; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!