Комбинированный метод хорд и касательных
Комбинированный метод основан на одновременном использовании методов хорд и касательных.
В результате получим две монотонные последовательности  - приближенные значения корня по недостатку и по избытку соответственно. Для нахождения корня
- приближенные значения корня по недостатку и по избытку соответственно. Для нахождения корня 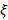 с заданной степенью точности достаточно ограничится теми значениями
с заданной степенью точности достаточно ограничится теми значениями  для которых
для которых  Так как
Так как  то в качестве значения корня следует взять среднее арифметическое чисел
то в качестве значения корня следует взять среднее арифметическое чисел  т. е. число
т. е. число

Легко видеть, что

Расчётные формулы:
а) если

на 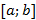 , то:
, то:

б) если

на 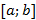 , то:
, то:
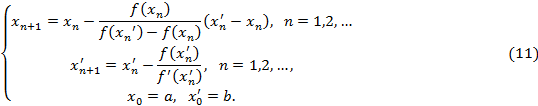
Метод простой итерации
Для использования этого метода исходное нелинейное уравнение записывается в виде

Пусть известно начальное приближение корня 
Подставляя это значение в правую часть уравнения  получаем новое приближение:
получаем новое приближение:  . Подставляя каждый раз новое значение корня в правую часть уравнения
. Подставляя каждый раз новое значение корня в правую часть уравнения  получаем последовательность значений:
получаем последовательность значений:

Итерационный процесс прекращается, если результаты двух последовательных итераций близки 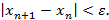
Достаточным условием сходимости метода простой итерации является условие  на множестве действительных чисел.
на множестве действительных чисел.
Достаточным условием сходимости метода простой итерации на отрезке 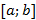 является условие
является условие 
Для более точной оценки погрешности используются формулы:
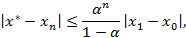

где

Примеры.
1.Дано уравнение 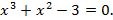 Исследовать вопрос о существовании и единственности корня
Исследовать вопрос о существовании и единственности корня 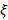 на отрезке
на отрезке  Вычислить три приближения корня уравнения по методу хорд и по методу касательных.
Вычислить три приближения корня уравнения по методу хорд и по методу касательных.
|
|
|
Решение.
Вычисляем знак выражения  где
где  . Т. к.
. Т. к.  и
и 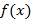 непрерывная функция на отрезке
непрерывная функция на отрезке  то уравнение имеет хотя бы один корень на заданном отрезке.
то уравнение имеет хотя бы один корень на заданном отрезке.
Для доказательства единственности корня вычисляем  и определим их знак на отрезке
и определим их знак на отрезке 

 на отрезке
на отрезке  следовательно,
следовательно, 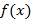 монотонно возрастает, и корень уравнения на отрезке
монотонно возрастает, и корень уравнения на отрезке  единственный;
единственный;  , следовательно, функция сохраняет на отрезке выпуклость. Т.к.
, следовательно, функция сохраняет на отрезке выпуклость. Т.к.  , то для вычисления приближенных значений корня по методу хорд используются формулы
, то для вычисления приближенных значений корня по методу хорд используются формулы  а по методу касательных
а по методу касательных 
Используя данные формулы, получаем ответ:
 –приближенные значения корня по методу хорд;
–приближенные значения корня по методу хорд;
 – приближенные значения корня по методу касательных.
– приближенные значения корня по методу касательных.
2Вычислить четыре приближения методом простой итерации для уравнения

Решение.
Для исследования выберем отрезок 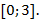
1) Функция

определена и имеет в каждой точке  из отрезка
из отрезка  производную
производную

2) Значения функции удовлетворяют неравенству:

т. е. все значения функции содержатся в отрезке 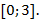
3) Производная функции удовлетворяет неравенству:
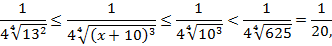
т. е. существует

такое, что для всех  из отрезка
из отрезка  имеет место неравенство:
имеет место неравенство:

Следовательно, выполнено достаточное условие применимости метода простой итерации на отрезке.
|
|
|
Выберем произвольно  из отрезка
из отрезка  например
например  Используя формулу
Используя формулу  получаем четыре приближенных значения корня:
получаем четыре приближенных значения корня:


Оценим погрешность четвертого приближения:

Дата добавления: 2018-04-15; просмотров: 918; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
