Каноническая форма двухслойных
Итерационных методов
Если при решении СЛАУ
Ax=b (3.22)
итерационным методом для вычисления вектора решений x(k+1) используется только значения предыдущей итерации x(k), то такой метод называется двухслойным или одношаговым. Если x(k+1) вычисляется через значения двух итерации x(k) и x(k-1) , то метод называется трехслойным или двухшаговым. Здесь рассмотрим только двухслойные методы.
Отметим, что важную роль в итерационных методах играет запись их в канонической форме. Для приведения (3.22) к канонической форме представим матрицу системы в виде
A=B-C, (3.23)
где В – невырожденная матрица.
Из (3.22) и (3.23) получим
x=B-1Cx+B-1b.
Тогда итерации можно проводить по формуле
x(k+1)=x(k)-B-1(Ax(k)-b) или
B(x(k+1)-x(k))+ Ax(k)=b. (3.24)
Для ускорения сходимости итерационных методов в формулу (3.24) водят числовые параметры, которые могут зависеть от номера итерации. Тогда вместо (3.24) используется
В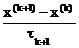 
+ Ax(k)=b, (3.25)
где t1, t2,…, tk+1,…-итерационные параметры.
tk+1>0 , k=0, 1, 2,…
Если В=Е – единичный оператор, то формула (3.25) примет вид
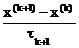+ Ax(k)=b.
Отметим, что в общем случае матрица В может зависеть от номера итерации k , ниже мы предполагаем, что матрица В не зависит от номера итерации.
|
|
|
Итерационный метод (3.25) называется стационарным, если tk+1=t не зависит от номера итерации, в противном случае – нестационарным.
Каноническая форма метода простой итерации
Для построения канонической формы метода простой итерации [9, 10] систему уравнений (3.22) запишем в виде
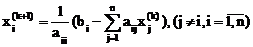, (3.26)
где aii¹0.
Второй член правой части (3.26) будет
, (3.27)
где D=[aii] – диагональная матрица.
Подставляя (3.27) в (3.26) получим
,
в матричной форме
x(k+1)-x(k)=D-1(b-Ax(k))
или в канонической форме
D 
+ Ax(k)=b, t=1, k=0, 1, 2,…
Каноническая форма метода Зейделя
Для решения системы (3.22) методом Зейделя, метод можно записать в следующей форме
, (3.28)
где aii¹0. Из формулы (3.28) получим формулы для последовательного вычисления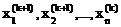 
(к=0, 1, 2,…)
. (3.29)
В матричной форме (3.29) примет вид
x(k+1)=D-1(b-Ux(k)-Lx(k+1)), (3.30)
где D – диагональная матрица, U и L – соответственно, верхняя и нижняя треугольные матрицы, так что
A=L+D+U. (3.31)
Из формул (3.30) и (3.31) после простых преобразований получим каноническую форму метода Зейделя [9, 11]
(D+L)(x(k+1)-x(k))+Ax(k)=b, (3.32)
|
|
|
где t=1, k=0, 1, 2,…
Для ускорения сходимости итерационного процесса, можно привести метод Зейделя (3.32) к методу релаксации, вводя итерационный параметр w, тогда имеем
(D+wL) 
+Ax(k)=b, k=0, 1, 2,… (3.33)
Отметим, что при 1<w<2 метод (3.33) называется верхней релаксацией, при 0<w<1 – нижней релаксацией, при w=1 – полной релаксацией или методом Зейделя.
Теоремы двухслойных итерационных методов
Двухслойные итерационные методы в канонической форме записываются в виде
В 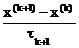+ Ax(k)=b, (3.34)
где В – вещественная невырожденная матрица, tk+1 – последовательность итерационных параметров, х(0) – произвольный начальный вектор.
Имея, вектор погрешности
z(k)=x(k)-x, где х – точное решение. Можно преобразовать (3.34), для этого значения
x(k+1)=z(k+1)+x, x(k)=z(k)+x подставляем в (3.34). Тогда получим
В 
+ Az(k)=0 (3.35)
у которого вектор погрешности z(k) является решением и условие сходимости итерационного процесса (3.34) может быть переписано так:
. (3.36)
Из (3.35) выделим вектор погрешности z(k+1)
z(k+1)=(E-tk+1B-1A)z(k)=Skz(k) ,
где Sk=E-tk+1B-1A – матрица перехода. Тогда
|
|
|
z(k)= Sk-1Sk-2…S1S0z(0)=Тk0z(0) ,
где Тk0= Sk-1Sk-2…S1S0 – разрешающая матрица.
При стационарном итерационном процессе, когда tk+1=t
S0=S1=…=Sk-1=S. Если S=S* , то 
.
Теорема 3.4 [8, 9]. Для сходимости стационарного итерационного процесса (3.34) с матрицей перехода S необходимо и достаточно, чтобы все собственные значения матрицы S были по модулю меньше единицы.
Доказательство
Пусть выполнено (3.36), тогда
. (3.37)
Так как начальное приближение х(0) в (3.34) произвольно, то из (3.37) получаем
. (3.38)
Пусть Т – некоторая неособенная матрица. Запишем матрицу S в канонической форме Жордана
S=TJT-1 ,
где
J= 
, a1+a2+…+am=n.
Здесь Jap – клетка Жордана порядка ap:
Jap= 
, где mp – собственные значения матрицы S. Тогда Sk=TJkT-1 . Поэтому из (3.38) следует, что
. (3.39)
Так как
,
то видно, что для выполнения (3.39) необходимо, чтобы ½mp½<1. Теорема доказана.
Теорема 3.5 [8, 9]. Для того, чтобы стационарный итерационный процесс (3.34) с матрицей перехода S сходился достаточно, чтобы норма матрицы S была меньше единицы.
Доказательство
|
|
|
Доказательство следует из того, что если 
, то и ½mp½<1. Следовательно, по теореме 3.4 стационарный итерационный процесс сходится.
Дата добавления: 2018-04-15; просмотров: 984; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!