Погрешности приближенных вычислений

⇐ ПредыдущаяСтр 2 из 13Следующая ⇒

Погрешности численного решения различных задач обусловлены следующими основными причинами:

1) неточностью математической модели, в частности неточно заданы исходные данные описания;

2) приближенным характером методов решения;

3) операции округления в вычислительной технике.

Погрешности, вызванные этими причинами, называют, соответственно:

А) неустранимой погрешностью,

Б) погрешностью метода,

В) вычислительной погрешностью.

Введем следующие обозначения:

х – точное значение параметра;

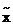- значение параметра, соответствующее принятой модели;

– значение численного решения, полученное по принятой модели, в предположении отсутствия ошибок округлений;

x_h – приближенное решение задачи, получаемое при реальных вычислениях.

Тогда

d₁=½ х - 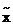½– неустранимая погрешность;

d₂=½ 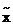- ½– погрешность численного решения;

d₃=½ - x_h½– погрешность вычисления.

Таким образом, полная погрешность равняется

d_о=d₁+d₂+d₃=½х- x_h½.

Определение 1.1. Если х точное значение, а x_h – приближенное значение некоторого параметра, то абсолютная погрешность D определяется формулой

D=½ х- x_h½.

Определение 1.2. Относительная погрешность d этого же параметра вычисляется по формуле

d=½ х- x_h½/½x_h½.

Обусловленность системы линейных алгебраических уравнений

Система линейных алгебраических уравнений (СЛАУ) в развернутой форме записывается следующим образом

(1.1)

Из теории линейной алгебры следует, что система уравнений (1.1) имеет решение (совместна) при любых правых частях в том и только в том случае, если соответствующая однородная система имеет только тривиальное решение х₁=х₂=…х_n=0. Необходимым и достаточным условием этого является условие, когда матрица А

имеет определитель, отличный от нуля, т.е. detA¹0. Условие совместности системы (1.1) при любых правых частях detA¹0 обеспечивает и единственность решения. С использованием матрицы А систему (1.1) можно переписать в виде

или в матричной форме

Ax=b. (1.2)

Пусть требуется найти решение системы (1.2). Задача решения системы (1.2) поставлена, корректна, если

1) решение задачи существует;

2) решение единственно;

3) решение непрерывно зависит от входных данных.

Известно, что требования 1 и 2 будут выполнены, если detA¹0. Требование 3 нуждается в детализации. Входными данными в задаче (1.2) являются коэффициеты a_ij матрицы А и компоненты вектора .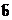

Если входные данные А и заданы с некоторой погрешностью dА, db, то вместо системы (1.2) решается задача

(А+dА)(х+dх)=b+db. (1.3)

Тогда возникает вопрос о том, как связана погрешность решения dх с погрешностями входных данных dА или db.

Пусть вначале dА=0, а db¹0. Тогда из формулы (1.3) получим

Ах+Аdх=b+db. (1.4)

После вычитания из (1.4) выражения (1.2) получим

Аdх=db,

dх=А^-1db,

следовательно

║dх║£║А^-1║║db║. (1.5)

Таким образом, связь между ║dх║ и ║db║ установлена. Однако на практике более естественна связь между нормами относительных погрешностей, а не абсолютных.

Так как

║b║£║А║║х║, (1.6)

то из (1.5) и (1.6) получим

║dх║║b║£║А║║А^-1║║х║║db║

или

║dх║/║x║£║А║║А^-1║║db║/║b║. (1.7)

Теперь пусть db=0, dА¹0. Дополнительно предположим, что dА таково, что

det(A+dА)¹0. Тогда из формулы (1.3) получим

х+dх=(A+dА)^-1b. (1.8)

После вычитания из (1.8) х= А^-1b получим

dх=[(A+dА)^-1-A^-1]b. (1.9)

Введем обозначение

B=(A+dА)

и используя тождество

B^-1- A^-1= A^-1(A-B)B^-1

находим, что

B^-1- A^-1= -A^-1dА(А+dА)^-1

или

(A+dА)^-1- A^-1= -A^-1dА(А+dА)^-1. (1.10)

После подстановки (1.10) в (1.9) получим

dх= -A^-1dА(А+dА)^-1b,

откуда

b= -dх/[ A^-1dА(А+dА)^-1] . (1.11)

После подстановки (1.11) в (1.8) получим

dх= -A^-1dА(х+dх)

или

║dх║£║А^-1║║dА║║х+dх║, (1.12)

║dх║/║x+dх ║£║А║║А^-1║║dА║/║А║. (1.13)

Из (1.5) и (1.12) следует, что если ║db║®0 или ║dА║®0, то ║dх║®0. Это и означает непрерывную зависимость решения задачи (1.2) от входных данных. Следовательно, условия detA¹0, det(A+dА)¹0 обеспечивают корректную постановку задачи (1.2).

Входящее в оценки (1.7) и (1.13) число n(А)=║А║║А^-1║ называется числом обусловленности матрицы А.

Определение 1.3. Если число n(А) относительно мало, то матрица А является хорошо обусловленной. Если число n(А) относительно велико, то матрица А является плохо обусловленной.

Для плохо обусловленной СЛАУ недопустима, велика правая часть в неравенствах (1.7) и (1.13). Поэтому лишь очень малые погрешности входных данных задачи (1.2) гарантируют приемлемую относительную погрешность решения.

Определение 1.4. Число n(А) для произвольной квадратной матрицы А удовлетворяет условию

n(А)³ max½l_A½/min½l_A½³1, (1.14)

где l_A– собственное число матрицы А.

Определение 1.5.Число n(А) для симметричной матрицы А удовлетворяет условию

n(А)= max½l_A½/min½l_A½=1.

Пример 1.1. Дана матрица

. (1.15)

Для оценки числа обусловленности этой матрицы воспользуемся формулой (1.14). Как известно собственные значения матрицы А являются корнями характеристического уравнения

det½A-lE½=0,

l²+4l+0,0003-0.

Далее получим l₁=-0,0001, l₂=-3,9999, откуда n(А)³½l₂½/l₁½=39999»4^.10⁴. Отсюда следует, что матрица А плохо обусловленная.

Пример 1.2. Рассмотрим уравнение Ах=b, где матрица А задана выражением (1.15), . Тогда точное решение .

Допустим вектор b задан с погрешностью, т.е. имеем , тогда получим решение . Оценим относительную погрешность решения при db¹0. Из примера 1.1 известно n(А) »4^.10⁴. Тогда несмотря на малость ║db║/║b║»1,4143^.10^-4 относительная погрешность решения велика, т.е. ║dх║/║x║»0,9618£n(А)║db║/║b║»5,6772.

Основные теоремы

В этом параграфе приводятся основные теоремы, которые имеют широкое применение в численных методах решения СЛАУ.

Теорема Адамара [1]. Если для матрицы А порядка n выполняется n неравенств

½a_kk½- >0, ( ), (1.16)

то матрица А является невырожденной.

Доказательство

Пусть матрица А- вырождена, т.е. detA=0. Тогда существуют такие числа х₁, х₂, …, х_n c максимальным ½x_k½>0, что выполняется

( ).

Также выполняется

½a_kk½½x_k½£ ½x_j½£½x_k½ ( ).

Далее сокращая на ½x_k½, получим

½a_kk½£ ( )

или ½a_kk½- £0, ( ). Следовательно, при выполнении неравенств (1.16) detA¹0, т.е. А – невырождена. Теорема доказана.

Теорема о LU разложении [9]. Пусть все главные миноры матрицы А n-го порядка отличны от нуля, то есть

а₁₁¹0, ¹0, …, detA¹0, (1.17)

тогда матрица А представима в виде

A=LU, (1.18)

где L – нижняя треугольная матрица, U – верхняя треугольная матрица.

Доказательство

Доказательство проведем по методу математической индукции. Для n=1 утверждение (1.18) выполняется так как a₁₁=l₁₁u₁₁ .

Тогда пусть теорема верна для матрицы A_n_-1 порядка (n-1), т.е.

A_n-1=L_n-1U_n-1 . (1.19)

Покажем, что (1.19) влечет за собой (1.18). Для этого представим матрицу А в следующем виде

А= = , (1.20)

где

А_n-1= , Z= , V= .

Дальше А будем искать в виде (1.18). Тогда имеем

A= 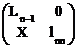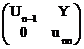= . (1.21)

Из (1.21) получаем

L_n_-1U_n_-1=A_n_-1 , L_n_-1Y=Z , XU_n_-1=V , XY+l_nnu_nn=a_nn . (1.22)

Первое из уравнений (1.22) выполняется из предположения (1.19). Так как detA_n_-1¹0 по условию (1.17), то матрицы L_n_-1 и U_n_-1 обратимы. Следовательно, из второго и третьего уравнений из (1.22) однозначно определяются вектор-столбец Y и вектор-строка Х.

Таким образом, остается определить только диагональные элементы l_nn и u_nn из четвертого уравнения. Это всегда можно сделать, приписав одному из чисел l_nn , u_nn произвольное и отличное от нуля значение, тогда второе число определится однозначно. Теорема доказана.

Отметим, что эта теорема является типичной теоремой существования, где доказано, что матрица А представима в виде (1.18), но не указан алгоритм построения треугольных матриц L , U.

Теорема 1.1 [7, 9]. Если матрица А имеет только простые собственные значения, то существуют преобразования подобия, приводящие её к диагональной форме.

Доказательство

Расположим n – линейно независимые собственные вектора матрицы А в столбцах матрицы Т

Т= . Тогда

АТ=А = =

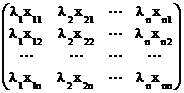= =ТL.

Т^-1АТ=L. Теорема доказана.

Отметим, что преобразование Т^-1АТ называется преобразованием подобия.

Теорема 1.2 [9]. Пусть detA¹0, тогда матрица А разлагается в произведение

A=QR, (1.23)

где Q – ортогональная матрица, R – верхняя треугольная матрица.

Доказательство

Для доказательства необходимо найти такое преобразование, которое ортогонализирует столбы матрицы А. Пусть a_i – столбцы матрицы А. Так как detA¹0, то система векторов a_i являются линейно независимой и образует базис в пространстве Rⁿ.

Тогда отыскание нужного преобразования сводится к задаче об ортогонализации базиса. Ортогональный базис будем строить с помощью алгоритма Грама-Шмита.

Пусть Q=(q₁, q₂,…, q_n) – искомая матрица с ортогональными столбцами q_i.

Положим a₁=q₁. Далее вектор а₂ разложим по ортогональным векторам q₁, q₂:

a₂=r₁₂q₁+q₂ , (q₁, q₂)=0, r₁₂=( q₁, a₂)/ (q₁, q₁).

Затем вектор а₃ разложим по ортогональным векторам q₁, q₂, q₃:

a₃=r₁₃q₁+ r₂₃q₂+q₃, (q₁, q₃)=0, (q₂, q₃)=0, r₁₃=(q₁, a₃)/(q₁, q₁), r₂₃=(q₂, a₃)/(q₂, q₂) и т.д.

Окончательно, получим

a_i=r₁_iq₁+ r₂_iq₂+…+r_i_-1,_iq_i_-1+q_i . (1.24)

Коэффициенты разложения (1.24) определяются из условий ортогональности (q_i, q_j)=0 при i¹j :

r_ij=(q_i, a_j)/(q_i, q_i), i<j.

Матричная запись (1.24) будет

A=Q =QR. Теорема доказана.

Для нахождения векторов q_i из (1.24) получим

q_i=a_i-r_1iq₁-r_2iq₂-…-r_i-1,Iq_i-1.

Теорема 1.3 [9]. Пусть detA¹0, тогда матрица А разлагается в произведение

A=QL,

где Q – ортогональная матрица, L – нижняя треугольная матрица.

Доказательство

Теорема доказывается аналогично теореме 1.2.

Дата добавления: 2018-04-15; просмотров: 296; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!