Вариационно-итерационные методы
В параграфе 3.4 рассматривались такие итерационные методы решения СЛАУ
Ax=b, (3.40)
в которых для задания итерационных параметров требовалось знание границы собственных значений матрицы А. Что делать, если такой информации нет? В таком случае можно применять методы, не использующие знания о границах собственных значений матрицы А.
Ниже описываются итерационные методы вида
В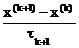 
+ Ax(k)=b, k=0, 1, 2,…
в которых параметры tk+1 выбираются из других условий.
Метод минимальных невязок
Рассмотрим явную схему метода минимальных невязок [8, 9] заданную формулой с симметричной положительно определенной матрицей А
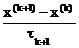+ Ax(k)=b, k=0, 1, 2,… (3.41)
Для невязки R(k)= Ax(k)-b из (3.41) получим
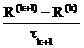+ AR(k)=0, k=0, 1, 2,…
R(k+1)=R(k)-tk+1AR(k) .
Параметр tk+1 выбираем из условия минимума невязки R(k+1) по норме
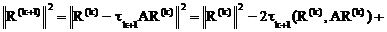
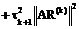=j(tk+1).
Дальше вычислим производную от функции j(tk+1) по параметру tk+1 и приравняем нулю
j’(tk+1)= -2(R(k),AR(k))+2tk+1 
=0
или
, k=0, 1, 2,… (3.42)
При этом значении параметра tk+1 вторая производная j”(tk+1)>0, следовательно, достигается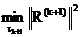 
.
В этом методе переход от k-ой итерации к (k+1)-ой осуществляется следующим образом. По найденному значению x(k) вычисляется вектор невязки R(k)= Ax(k)-b и по формуле (3.42) находится параметр tk+1. Затем по формуле (3.41) вычисляется вектор x(k+1).
Метод минимальных невязок (3.41), (3.42) сходится с той же скоростью, что и метод простой итерации с оптимальным параметром t .
|
|
|
Метод скорейшего спуска
В методе скорейшего спуска [8, 9], в явной схеме (3.41), итерационный параметр tk+1 выбирается из условия минимума нормы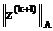 
вектора погрешности z(k+1)=x(k+1)-x. Так как погрешность z(k+1) удовлетворяет уравнению
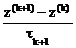+ Az(k)=0, k=0, 1, 2,…
или
z(k+1)= z(k)-tk+1Az(k) ,
то имеем
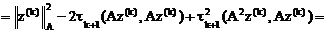Y(tk+1).
Дальше находим производную от функции Y(tk+1) по параметру tk+1 и приравняем к нулю, тогда
Y’(tk+1)= -2(Az(k), Az(k))+2tk+1(A2z(k), Az(k))=0
или
.
Так как вектор погрешности z(k)=x(k)-x неизвестен, поскольку неизвестно точное решение х. Тогда с учетом того, что
Az(k)=Ax(k)-Ax=R(k)
вычисление tk+1 можно проводить по формуле
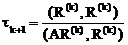. (3.43)
Отметим, что метод скорейшего спуска (3.41), (3.43) сходится со скоростью метода простой итерации с оптимальным параметром t.
Глава 4. Методы решения задач на
Собственные значения
На практике часто возникают различные требования к информации о собственных значениях и собственных векторах матриц:
1. При решении задач механики, физики и химии требуется нахождение всех собственных значений и векторов матриц. Такую задачу называют полной проблемой собственных значений;
|
|
|
2. Иногда требуется найти максимальное или минимальное по модулю собственное значение матрицы. Такого рода задачи возникают при решении некоторых задач ядерной физики
3. При исследовании колебательных процессов иногда требуется найти два максимальных по модулю собственных значений матрицы. Подобные задачи называют частичной проблемой собственных значений.
Таким образом, алгебраическая проблема собственных значений состоит в определении тех собственных значений l, при которых система n однородных линейных уравнений с n неизвестными
Ах=lх, х¹0 (4.1)
имеет нетривиальное решение.
Отметим, что если матрицу А с помощью преобразований подобия Т-1АТ (согласно теорема 1.1) привести к диагональной матрице D, то полная проблема собственных значений будет решена.
Действительно, если D подобна А, то
D= Т-1АТ, (detT¹0) (4.2)
DY=gY. (4.3)
Умножим (4.2) справа на вектор Y
DY= Т-1АТY,
теперь умножим слева на Т
ТDY=АТY,
тогда с учетом (4.3)
А(ТY)=g(ТY).
Откуда видно, что собственное значение g матрицы D совпадает с собственным значением l матрицы А, а собственный вектор Y матрицы D связан с собственным вектором х матрицы А соотношением
|
|
|
х=ТY.
Определение 4.1. Собственные значения диагональной матрицы D равны диагональным элементам, т.е. g1=d11, g2=d22,…, gn=dnn.
Определение 4.2. Собственные значения треугольной (верхней или нижней) матрицы совпадают с диагональными элементами, т.е. l1=d11, l2=d22,…, ln=dnn.
Определение 4.3. Для вещественной симметричной матрицы А собственные значения вещественны, а собственные вектора, соответствующие различным собственным значениям ортогональны.
Определение 4.4. Если матрицы А и В удовлетворяют тождеству
(Ах, у)=(х, Ву), (4.4)
то матрица В называется сопряженным матрице А и обозначается A*.
В дальнейшем (4.4) будем записывать в виде
(Ах, у)=(х, A*у), (4.5)
которое называется тождеством Лагранжа.
Наряду с задачей (4.1) также рассматривается задача
A*у=hу, у¹0. (4.6)
Так как det(A*-hE)=det(A-lE) следует, что l=h. Следовательно, вместо (4.6) можно написать
|
|
|
A*у=lу.
Дата добавления: 2018-04-15; просмотров: 430; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!