Методы для матриц, не принадлежащих

К специальному классу

Здесь будут рассмотрены методы решения полной проблемы собственных значений для несимметричных матриц, при этом не делается каких-либо оговорок относительно кратности или не кратности собственных значений. К таким методам относятся QL и QR алгоритмы [9, 11, 12]. Отметим, что эти алгоритмы являются типичными представителями методов трансформационного типа. Общая идея этих методов состоит в том, чтобы посредством последовательности простых преобразований подобий привести матрицу к той или иной канонической форме, позволяющей без труда определить собственные значения и вектора.

QL – алгоритм

Пусть detA¹0, тогда согласно теореме 1.3 матрицу А можно разложить

A=QL,                                                                       (4.34)

где Q – ортогональная матрица, L – нижняя треугольная матрица. Тогда матрица В, равная

B=LQ=Q^TAQ=Q^-1AQ,                                              (4.35)

подобна матрице А.

Дальше, согласно формуле (4.35) формируется последовательность подобных матриц

A₁=A; A₁=Q₁L₁ , A₂=L₁Q₁= 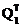A₁Q₁ ,

        A₂=Q₂L₂ , A₃=L₂Q₂= 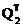A₂Q₂ ,                   (4.36)

         ……………………………….

        A_k=Q_kL_k , A_k+1=L_kQ_k= 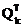A_kQ_k .

Формула (4.36) описывает QL – алгоритм без сдвигов. При к®¥ последовательность матриц А_k+1 сходятся к треугольной. Их диагональные элементы стремятся к её собственным значениям, которые в свою очередь являются собственными значениями матрицы А.

Наддиагональный элемент (A_k)_ij матрицы A_k на к-ой итерации QL – алгоритма равен s_ij(l_i/l_j)^k , где s_ij – постоянная и ½l₁½<½l₂½<…<½l_n½.

Отметим, что сходимость QL – алгоритма улучшится, если использовать сдвиги.

 

QR – алгоритм

Пусть detA¹0, тогда согласно теореме 1.2 матрицу А можно представить в виде

A=QR,                                                                       (4.37)

где Q – ортогональная матрица, R – верхняя треугольная матрица. Тогда матрица В, равная

B=RQ=Q^TAQ=Q^-1AQ,                                             (4.38)

подобна матрице А.

Согласно, формуле (4.38) составляется последовательность подобных матриц

A₁=A; A₁=Q₁R₁ , A₂=R₁Q₁= 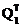A₁Q₁ ,

        A₂=Q₂R₂ , A₃=R₂Q₂= 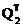A₂Q₂ ,                  (4.39)

         ……………………………….

        A_k=Q_kR_k , A_k+1=R_kQ_k= 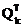A_kQ_k .

В общем случае, когда собственные значения матрицы А различны, последовательность матриц A_k имеет пределом верхнюю треугольную матрицу А_¥ , диагональные элементы которой представляют собой собственные значения исходной матрицы. Формула (4.39) описывает QR – алгоритм без сдигов.

Модификация вида A₁=A,…, A_k-a_kE=Q_kR_k , A_k+1=R_kQ_k+a_kE = 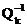A_kQ_k , где a_k – величина сдвига называется QR – алгоритмом со сдвигом сходимость, которого существенно выше по сравнению с QR – алгоритмом.

 

Обобщенная задача на собственные значения

Обобщенная задача на собственные значения [13] очень важна для приложений. Эта задача задается уравнением

Ах=lВх.                                                                   (4.40)

Если матрица В положительно определена, то для задачи (4.40) справедливы:

1) Все её собственные значения вещественны;

2) Собственные значения имеют тот же знак, что и собственные значения задачи Ах=lх.

 

Обобщенный метод Якоби

Метод предназначен для решения задачи (4.40). Очевидно, что обобщенная задача на собственные значения (4.40) эквивалентна для любой невырожденной матрицы Т задачи: TАT^Ty=lTВT^Ty ,

причем новая задача сохраняет свойства исходных матриц А и В такие как симметричность и положительная определенность. В качестве матрицы Т выбираются:

                       i                      j

T_ij(k)= , (i<j).

Видно, что элементы на месте (i, j) у матриц T_ij(k)А 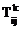(k) и T_ij(k)В 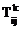(k) определяются по формулам:

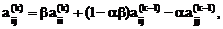
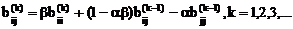
Обобщенный метод Якоби для задачи (4.40) состоит в последовательном применении конгруэнтных преобразований матриц А и В с помощью матриц T_ij(k) таких, что на каждом шаге 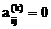, 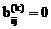. В качестве стратегии выбора зануляемых элементов может быть реализован один из вариантов обычного метода Якоби (см. параграф 4.2).

Значения параметров a, b матриц T_ij(k) определяются из соотношений:

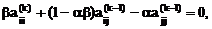
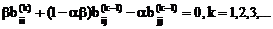
Обозначая через с=(1-ab) получим две системы линейных алгебраических уравнений:

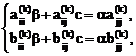
и                                                                                       (4.41)

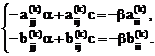
По правилу Крамера из этих уравнений получим:

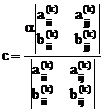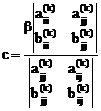, .                            (4.42)

Обозначая через:

, ,

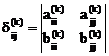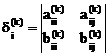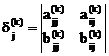
и приравнивая правые части (4.42) получим:

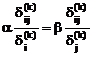.                                                          (4.43)

Положив, 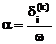 из (4.43) получим .

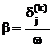После подстановки этих выражений для a и b в одно из исходных уравнений (4.41), получим:

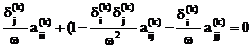
или

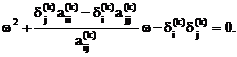                       (4.44) 

После упрощений (4.44) примет вид:

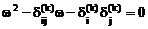.                                            (4.45)

Когда матрица В положительно определена, уравнение (4.45) имеет ненулевое решение. Чтобы a и b были достаточно малыми величинами, в качестве w нужно выбирать тот корень уравнения, который дальше отстоит от нуля.

После вычисления w элементы матрицы T_ij(k) определяются по формулам:

 , .

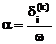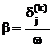На обобщенный метод Якоби распространяется квадратичная сходимость обычного метода Якоби, при условии, что итерационный процесс вообще сходится. Отметим, что теоретически сходимость обобщенного метода Якоби ещё не доказана [13].

 

---

Дата добавления: 2018-04-15; просмотров: 233; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!