Устойчивость задачи на собственные значения
Для простоты будем считать, что все собственные значения матрицы А простые в задаче (4.1).
На практике элементы матрицы А, почти всегда, заданы с некоторой погрешностью dА, тогда вместо (4.1) будем иметь
(А+dА)(х+dх)=(l+dl)(х+dх),
тогда отбросив, члены второго порядка малости получим
Ах+dАх+Аdх=lх+dlх+ldх
из последнего выражения вычтем (4.1), тогда имеем
dАх+Аdх=dlх+ldх. (4.7)
Рассмотрим два варианта существования погрешностей:
1) dх=0, dl¹0;
2) dх¹0, dl=0.
Последовательно рассмотрим оба варианта.
Вариант 1. dх=0, dl¹0.
Тогда из (4.7) имеем
dАхi=dliхi ,
(yi, dАхi)=dli(yi, xi),
.
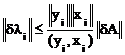Отношение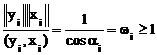 
называется i-ым коэффициентом перекоса матрицы А, где ai – угол между собственными векторами xi и yi .
Таким образом,
.
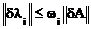Следовательно, если погрешность dА мала и мал i-ый коэффициент перекоса, то мала погрешность определяемого i-го собственного значения.
Отметим, что для симметричной матрицы все wi=1, поэтому задача нахождения собственных значений симметричной матрицы является устойчивой.
Вариант 2. dх¹0, dl=0.
Тогда из (4.7) имеем
Аdхi +dАхi =lidхi ,
(Аdхi, yj)+(dАхi, yj)= li(dхi, yj) , (4.8)
где (Аdхi, yj)=( dхi, A*yj)=(dхi, ljyj)=lj(dхi, yj).
Подставляя последнее в (4.8) получим
lj(dхi, yj)+(dАхi, yj)= li(dхi, yj),
(dхi, yj)=(dАхi, yj)/(li-lj), при i¹j. (4.9)
Пусть
dхi=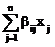 
, (4.10)
тогда
(dхi, yj)=bij(xj, yj)
|
|
|
после подстановки этого выражения в (4.9) получим
bij=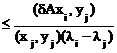 
при i¹j,
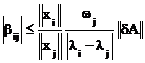. (4.11)
Из (4.10), (4.11) видно, что если мала погрешность определения элементов матрицы А и малы все коэффициенты перекоса, то мала погрешность определения i-го собственного вектора, соответствующего i-му собственному значению.
Следствие 4.1. Если матрица А=A* и все собственные значения простые, то задача нахождения собственных векторов устойчива.
Метод вращения Якоби
Метод Якоби [4, 5, 9, 11] применяется для решения полной проблемы собственных значений симметричных матриц. Пусть А – исходная симметричная матрица, имеющая простые собственные значения. Тогда согласно теореме 1.1 имеем
Т-1АТ=L, (4.12)
где L - диагональная матрица. В качестве матрицы Т используем ортогональную матрицу вращения
i j
Tn(i,j)= 
, (i<j).
Так как Tn – ортогональная матрица (4.12) запишется в виде
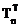АТ=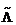 
, (4.13)
где 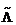- квазидиагональная матрица.
Дальше строится последовательность матриц Аn при начальной А0=А:
|
|
|
А1=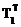 
А0Т1 ,
…………. , n=1, 2, 3,… (4.14)
Аn= 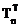Аn-1Тn .
При n®¥ limAn=L.
Идея построения последовательности (4.14) такова:
допустим, что ненулевой, недиагональный элемент матрицы Аn-1 находится в позиции (i, j), тогда умножение её на Тn справа и 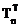слева соответствует вращения матрицы Аn-1 в плоскости (i, j). Угол вращения q выбирается таким образом, чтобы сделать элемент (i, j) матрицы Аn нулевым.
Алгоритм метода вращения, который получается из последней строки последовательности (4.14), будет таким:
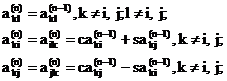
(4.15)
где c=cosq, s=sinq, n=1, 2, 3,…
Из последнего выражения формул (4.15) получим
tg2q=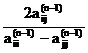 
, ½q½£p/4. (4.16)
Из исходных соотношений получим уравнение
tgq=s/c=t. (4.17)
Далее из (4.16), (4.17) получим
t2+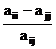 
t-1=0. (4.18)
Для сходимости и устойчивости метода необходимо выбрать наименьший по модулю корень уравнения (4.18). Зная t можно вычислить с, s:
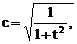s=tc.
Для якобиева вращения,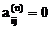 
, справедливо
t2(An)= t2(An-1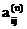)-2( 
)2 ,
где
t2(An-1)=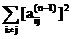 
.
Сходимость метода Якоби можно оценить числом t2(An), если процесс сходится, то t2(An)®0 при n®¥.
Процесс итерации заканчивается, когда все недиагональные элементы матрицы А удовлетворяют условию
|
|
|
½ 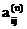½<e, i¹j , 0<e<1.
Наконец, о нахождении собственных векторов.
Пусть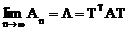 
, где Т= 
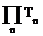, тогда столбцы матрицы Т будут собственными векторами матрицы А.
Заметим, так как метод Якоби носит итерационный характер, то элемент, который был сделан нулевым при следующем вращении, вообще говоря, может стать ненулевым.
Вопрос, в каком порядке занулять элементы матрицы А, т.е. вопрос о выборе индексов i и j для каждого шага, определяет различные варианты метода Якоби.
Дата добавления: 2018-04-15; просмотров: 370; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!