Алгоритм вычисления определителя матрицы

Определение 2.2. Если все главные миноры матрицы А n-го порядка отличны от нуля, то есть

а₁₁¹0, ¹0, …, detA¹0,                                     (2.11)

то проведение процесса исключения без перестановок гарантируется.

 

Определение 2.3. Если для матрицы А условия (2.11) выполнены, то определитель этой матрицы равен произведению ведущих элементов в методе последовательного исключения Гаусса.

 

Пусть выполнены условия (2.11), тогда

detA=a₁₁ ,                                   (2.12)

где a_1j=a_1j/a₁₁, (j>1).

Дальше поступаем, как в методе Гаусса. Первую строку определителя (2.12) умножаем на а₂₁ и вычитаем из второй строки. Затем первую строку определителя (2.12) умножаем на а₃₁ и вычитаем из третьей строки и т.д. (такие преобразования не изменяют величины определителя). Тогда получим

detA=a₁₁ =а_{11 .}

Дальше повторим, тогда будем иметь

detA=a₁₁ ,                            (2.13)

где a_2j= / , (j>2).

Дальше, первую строку определителя (2.13) умножаем на   и вычитаем из второй строки. Затем первую строку определителя (2.13) умножаем на   и вычитаем из третьей строки и т.д. Тогда получим

detA=a₁₁ = a_{11 .}

Повторим описанную выше процедуру, тогда получим

detA=a₁₁ = a₁₁

и т.д. пока не получим

detA=a₁₁ ._….  ,                                               (2.14)

где = - a_к-1к , a_к-1к= /  ,  

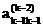  (k=2, 3,…,n).

 

Замечание 2.2. Если при   detA¹0 условия (2.11) не выполнены, то реализация процесса исключения включает в себя перестановки соответствующих строк. При этом измениться только знак определителя, так как перестановка двух строк влечет перемену знака определителя. Для сохранения нужного знака определителя надо в формуле (2.11) приписывать нужный знак ведущим элементам, которые вычислялись с перестановкой строк.

 

Алгоритм вычисления обратной матрицы

Из линейной алгебры известно, что

АА^-1=Е ,                                                                   (2.15)

где Е – единичная матрица, А^-1 – обратная матрица.

Если обозначить i-й  столбец обратной матрицы через y_i= , а i-й  столбец единичной матрицы через е_i= , то (2.15) можно переписать в виде

АА^-1=(Ау₁, Ау₂,…, Ау_n)=(е₁, е₂,…, е_n)=Е или 

Аy_i=e_i , (i=1, 2, …, n).

Рассмотрим расширенную матрицу

.                      (2.16)

Процесс исключения (прямой ход) будем проводить для всех строк расширенной матрицы (2.16).

Пусть а₁₁¹0, тогда первая строка матрицы (2.16) будет такой после деления на а₁₁

(1, a₁₂, a₁₃,…, a_1n, b₁₁, b₁₂,…, b_1n ),                        (2.17)

где a_1j=a_1j/a₁₁, (j>1), b_1j=e_1j/a₁₁ , (j³1).

С помощью строки (2.17) исключим все элементы первого столбца a_i1 матрицы (2.16) для которых i>1. В результате получим

,               (2.18)

где =a_ij-a_i1a_1j , (i, j³2), =e_ij-e_i1b_1j , (i³2, j³1).

На следующем этапе разделим вторую строку матрицы (2.18) на ¹0, тогда эта строка примет вид

(0, 1, a₂₃, a₂₄,…, a_2n, b₂₁, b₂₂,…, b_2n ),                    (2.19)

где a_2j= / , (j>2), b_2j= /  , (j³1).

Используя строку (2.19) исключим все элементы второго столбца  при i>2 матрицы (2.18). Тогда получим

,

где = - a_2j , (i, j³3), = - b_2j , (i³3, j³1).

Продолжая, таким образом, окончательно получим

,

где a_kj= / , (j³k+1), b_kj= /  , (j³1),

= - a_kj , (i, j³k+1), = - b_kj , (i³k+1, j³1).

На этом заканчивается процесс исключения – прямой ход. Дальше реализуется обратный ход, для этого решается система уравнений

= , (i=1, 2,…,n),

что позволяет найти все столбцы обратной матрицы А^-1

у₁= ,…, y_n= .

 

Метод Халецкого

При решении системы уравнений Ax=b методом Халецкого [2-4, 10,11] используется «теорема о LU разложении» (см. §1.3) согласно которой можно написать

A=LU,                                                                       (2.20) 

где 

L= , U= .

Тогда согласно формуле (2.20) элементы l_ij , u_ij определяются по формулам

(i³j>1).                                           (2.21)

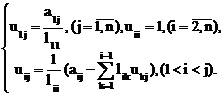                                (2.22)

Далее искомый вектор х вычисляется решением двух систем уравнений

Ly=b,

Ux=y.

Так как матрицы L и U треугольные, эти системы решаются по формулам

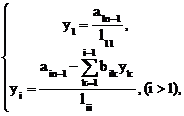                                       (2.23)

где a_in+1=b_i , (i=1,…,n).

                                            (2.24)

Формулы (2.21)-(2.24) составляют алгоритм метода.

 

Метод квадратных корней

Метод квадратных корней [2, 3, 11] применяется при решении системы уравнений

Ах=b,                                                                       (2.25)

когда матрица А – симметричная, т.е. А=А^Т , (a_ij=a_ji). При detA¹0 согласно «теореме о LU разложении» (см. §1.3) можно записать A=LU, где U=T, L=T^T. Тогда

А=Т^Т Т,                                                                     (2.26)

где

Т= , Т^Т= .

Расписывая, формулу (2.26) получим формулы для вычисления t_ij

Отсюда находим

                                               (2.27)

Система линейных алгебраических уравнений (2.25) имеет единственное решение, если t_ii¹0 (i=1,…,n), так как detA=(detT)²=(t₁₁^.t₂₂^. _… ^.t_nn)²¹0.

Используя, формулу (2.26) систему уравнений (2.25) можно переписать в виде двух систем уравнений

Т^Тy=b,                                                                      (2.28)

Тх=у.                                                                        (2.29)

Расписывая, систему уравнений (2.28) получим

                                       (2.30)

 

Расписывая, систему уравнений (2.29) получим

                                         (2.31)

Из формулы (2.30) находим

                                      (2.32)

Из формул (2.31) определяем неизвестные

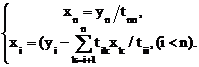                                       (2.33)

Формулы (2.27), (2.32) и (2.33) составляют алгоритм метода квадратных корней.

 

Метод прогонки

Метод прогонки [9, 11] предназначен для решения системы линейных уравнений

Ax=b,                                                                         (2.34)

когда матрица А – трехдиагональная и ненулевые элементы определяются следующим образом: a_ij¹0, если j=i-1, j=i, j=i+1.

Введем обозначения

a_ii-1=-a_i , a_ii=c_i , a_ii+1=-d_i .

Тогда система уравнений (2.34) запишется в виде

                              (2.35)

Решение (2.35) будем искать в виде

x_i=a_ix_i+1+b_i ,                                                             (2.36)

где a_i, b_i–неизвестные прогоночные коэффициенты.Подставив, найденные из (2.36) x_i-1 в среднее уравнение из системы (2.35), получим для 2£i£n-1 :

                                  (2.37)

Из сравнения (2.36) и (2.37) следует, что

                                       (2.38)

Зная a₁,b₁ по формулам (2.38) можно найти все  a_i, b_i   для i=2, 3,…, n, то есть провести прямой ход прогонки.

Если удастся найти x_n , то по формуле (2.36) при известных a_i, b_i   можно вычислить неизвестные  x_i   для i=n-1, n-2,…, 1, то есть провести обратный ход прогонки. Поэтому дальше определяем a₁,b₁ и x_n.

Из первого уравнения системы (2.35) найдем

чтовместе с уравнение

х₁=a₁х₂+b₁

из (2.36) при i=1 дает

                                                     (2.39)

Далее, из последнего уравнения системы (2.35) и из (2.36) при i=n-1 имеем систему уравнений

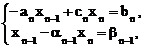
откуда находим

                                                    (2.40)

Таким образом, алгоритм метода прогонки при решении СЛАУ (2.35) заключается в следующем:

1) по формулам (2.39) и (2.38) вычисляются коэффициенты a_i, b_i для i=1, 2,…,n (прямой ход);

2) по формулам (2.40) и (2.36) вычисляются неизвестные x_i   для i=n-1, n-2,…, 1 (обратный ход).

Метод прогонки реализуется, если нет деления на нуль в формулах (2.38)-(2.40). Для выполнения этого условия достаточно, чтобы detA¹0.

Так как при использовании метода прогонки заранее неизвестен detA, тонеобходим простой способ оценки устойчивости метода.

Достаточные условия устойчивости метода прогонки. Для устойчивости метода прогонки достаточно выполнение неравенств:

Рассмотренный здесь вариант метода прогонки называется правой прогонкой. Название метода следует из того, что при обратном ходе неизвестные x_i вычисляются справа налево, т.е. сначала x_n , x_n-1 и т.д.

Существует метод левой прогонки, в котором неизвестные x_i вычисляются слева направо, т.е. сначала х₁ , х₂ и так далее.

Комбинация левой и правой прогонок дает метод встречных прогонок.

---

Дата добавления: 2018-04-15; просмотров: 270; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!