Глава 2. Прямые методы решения систем линейных

Алгебраических уравнений

Итак, требуется решить систему линейных алгебраических уравнений

Ax=b. (2.1)

Заметим, что везде речь будет идти только о случае когда матрица А – квадратная, т.е. число уравнений совпадает с числом неизвестных, причем будет предполагаться, что система (2.1) имеет единственное решение.

Методы решения (2.1) можно разделить на две группы: прямые методы (в которых нахождение решения заканчивается за конечное число действий), итерационные методы (в которых находятся не само решение, а некоторая последовательность векторов х^(к) такая, что ).

Метод Гаусса

Рассмотрим классический метод Гаусса [2-11]. Сначала перепишем систему (2.1) в развернутой форме

(2.2)

Пусть а₁₁¹0. Если а₁₁=0, то поменяем местами первое и второе уравнения в (2.2), если а₂₁¹0, то поменяем местами первое и третье уравнения и т.д. Все a_i₁ не могут равняться нулю, так как detA¹0. Тогда из первого уравнения системы (2.2) будем иметь

х₁+a₁₂х₂+…+a_1nх_n=b₁ , (2.3)

где a_1j=a_1j/a₁₁ , (j>1), b₁=b₁/a₁₁ .

С использованием уравнения (2.3) можно исключить х₁ из всех оставшихся уравнений (2.2). В результате получим

(2.4)

где =a_ij-a_i1a_1j, =b_i- a_i1b₁ , (i, j³2).

На этом первый этап процесса исключения заканчивается. Индекс (1) в коэффициентах , показывает номер первого этапа.

Переходя к второму этапу процесса исключения разделим первое уравнение в (2.4) на при ¹0, тогда получим

х₂+a₂₃х₃+…+a_2nх_n=b₂ , (2.5)

где a₂_j= / , (j>2), b₂= / .

Далее с помощью уравнения (2.5), описанным выше способом, исключим все х₂ из уравнений (2.4).

Продолжая далее, на к-ом этапе будем иметь уравнение, с помощью которого исключим к-ое неизвестное, т.е.

х_к+a_{к к+1}х_к+1+…+a_к_nх_n=b_k , (2.6)

где a_к_j= / , (j³к+1), b_к= / , (2.7)

= - a_к_j, = - b_к , (i, j³к+1). (2.8)

Собирая уравнения (2.3)-(2.6), полученных на всех этапах получим систему уравнений с верхней треугольной матрицей

х₁+a₁₂х₂+a₁₃х₃+…+a_1nх_n=b₁ ,

х₂+a₂₃х₃+…+a_2nх_n=b₂ , (2.9)

………………………

х_n=b_n .

Таким образом, алгоритм решения СЛАУ классическим методом Гаусса состоит из двух шагов:

1) первый – прямой ход.

По формулам (2.7), (2.8) вычисляются коэффициенты a_ij и b_i (i, j=1,…, n).

2) второй – обратный ход.

Определяются неизвестные x_i по формуле (2.9), которую можно записать в виде

x_i=b_i - , (i=n, n-1,…,1).

Определение 2.1. Элементы а₁₁, , …, ,… называются ведущими элементами.

Метод Гаусса с выбором главного элемента

При численных вычислениях на компьютере неизбежны ошибки округления, следовательно, есть возможность прекращения выполнения алгоритма или получение неверных результатов, если знаменатели дробей на каком-то этапе окажутся равными нулю или очень маленькими числами. Этого недостатка можно избежать, если использовать метод Гаусса с выбором главного элемента [11]. Рассмотрим систему уравнений

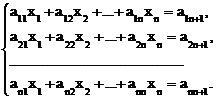
Запишем расширенную матрицу коэффициентов

. (2.10)

Среди элементов матрицы a_ij выберем наибольший по модулю, который называется главным элементом. Пусть им будет элемент a_ij и используя его вычислим множители

m_k= -a_kj/ a_ij для всех k¹i .

Строка с номером i матрицы М, содержащая главный элемент, называется главной строкой.

Далее, производим следующее действие: к каждой неглавной строке прибавляем главную строку, умноженную на соответствующий множитель m_k для этой строки. В результате получим новую матрицу, у которой j-й столбец состоит из нулей, кроме одного элемента. Отбрасывая этот столбец и главную i-ю строку, получим новую матрицу М⁽¹⁾ и повторяем ту же операцию, только с новым главным элементом, после чего получим матрицу М⁽²⁾ и т.д.

Таким образом, построим последовательность матриц М, М⁽¹⁾, М⁽²⁾,…, М⁽^n-1), последняя из которых представляет двучленную матрицу – строку, её также считаем главной строкой.

Затем объединяем в систему все главные строки, начиная с последней, входящей в матрицу М⁽^n-1). После некоторой перестановки строк они образуют треугольную матрицу эквивалентную матрице (2.10). На этом заканчивается – прямой ход.

Решив систему с треугольной матрицей, последовательно находим все неизвестные – обратный ход.

Замечание 2.1. При работе с матрицами большого порядка выбор главного элемента может оказаться достаточно трудоемкой задачей. Поэтому на практике, в качестве главного элемента, выбирают первую строку, а.в качестве главного элемента наибольший по модулю элемент этой строки.

Дата добавления: 2018-04-15; просмотров: 212; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!