Глава 3. Итерационные методы решения систем
Линейных алгебраических уравнений
В главе будут описаны итерационные методы решения систем линейных алгебраических уравнений
Ax=b. (3.1)
При решении системы уравнений (3.1) итерационным методом отыскивается последовательность векторов x(k) такая, что
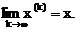 (3.2)
(3.2)
Введем понятие вектора погрешности
z(k) =x(k)-x (3.3)
и вектора невязок
R(k)=Ax(k)-b . (3.4)
Из формулы (3.2) следуют, что
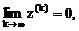
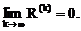
Отметим, что в отличие от вектора погрешности z(k) вектор невязок R(k) может быть вычислен. Поэтому очень часто в качестве условия окончания итераций выбирают
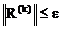 , где 0<e<1. (3.5)
, где 0<e<1. (3.5)
Условие (3.5) является не вполне корректным, покажем это. Действительно, из (3.3) имеем
Az(k)=Ax(k)-b= R(k) ,
z(k)=A-1 R(k) ,

С другой стороны
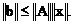
Следовательно,

или
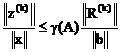 , (3.6)
, (3.6)
где  – число обусловленности матрицы А. Из (3.6) следует, что лишь для хорошо обусловленных систем (3.1) относительная малость векторов невязок R(k) влечет за собой относительную малость векторов погрешности z(k). Для таких задач условие (3.5) является корректным.
– число обусловленности матрицы А. Из (3.6) следует, что лишь для хорошо обусловленных систем (3.1) относительная малость векторов невязок R(k) влечет за собой относительную малость векторов погрешности z(k). Для таких задач условие (3.5) является корректным.
Для плохо обусловленной системы (3.1) относительная малость векторов невязок R(k) не влечет относительную малость векторов погрешности z(k). Для таких задач условие (3.5) является не вполне корректным.
|
|
|
Метод простой итерации
Для описания метода простой итерации [2-4, 6, 11] распишем систему (3.1)
 (3.7)
(3.7)
Полагая, что коэффициенты aii¹0 (i=1, 2,…, n) разрешим первое уравнение из (3.7) относительно х1 , второе относительно х2 и т.д. Тогда получим
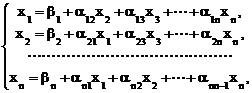 (3.8)
(3.8)
где bi=bi/aii , aij=-aij/aii при i¹j, aij=0 при i=j,
(i,j=1, 2,…,n).
Вводя обозначения
 ,
, 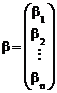 ,
, 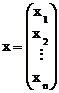
перепишем систему уравнений (3.8) в матричной форме
х=b+aх . (3.9)
Систему уравнений (3.9) будем решать методом последовательных приближений. За нулевое приближение примем столбец свободных членов
х(0)=b ,
где индекс (0) – номер нулевого приближения.
Дальше строим последовательность
х(1)= b+aх(0) ,
х(2)= b+aх(1) ,
………….. (3.10)
х(k+1)= b+aх(k) .
Если последовательность приближений х(0) , х(0) ,…, х(k) ,… имеет предел 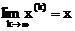 , то этот предел будет решением системы уравнений (3.8).
, то этот предел будет решением системы уравнений (3.8).
Таким образом, алгоритм метода простой итерации для решения СЛАУ будет следующим
|
|
|
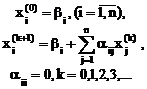
Итерация заканчивается при выполнении условия
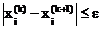 ,
,  где 0<e<1.
где 0<e<1.
3.1.1. О сходимости итерационных процессов для систем линейных алгебраических уравнений
Теория сходимости итерационных процессов для решения СЛАУ разработана достаточно хорошо. Здесь ограничимся рассмотрением нескольких достаточных условий сходимости.
Теорема 3.1 [3]. Процесс итерации для приведенной линейной системы (3.9) сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы a меньше единицы, т.е. для итерационного процесса
х(k)= b+aх(k-1) (k=1,2,…)
достаточное условие сходимости есть
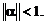
Доказательство.
При заданном произвольном векторе х(о) , имеем последовательность приближений
х(1)= b+aх(о),
х(2)= b+aх(1),
……………
х(k)= b+aх(k-1).
Откуда
х(k)=(Е+a+a2+…+ak-1)b+akх(o). (3.11)
Так как 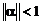 , то
, то 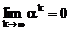 и
и
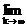 (Е+a+a2+…+ak-1)=
(Е+a+a2+…+ak-1)= 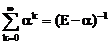 ,
,
которое следует из [3] (см. теорема 5, стр. 250).
Следовательно,
х= 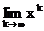 =(Е-a)-1b. Теорема доказана.
=(Е-a)-1b. Теорема доказана.
Следствие 3.1. Процесс итерации для системы (3.9) сходится, если:
а) 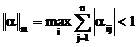 ,
,
б) 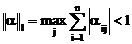 ,
,
в) 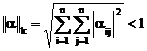 .
.
Следствие 3.2. Для системы уравнений
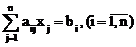
процесс итерации сходится, если выполнены условия теоремы Адамара.
Дата добавления: 2018-04-15; просмотров: 258; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
