Параллельность прямой и плоскости. Признак параллельности прямой и плоскости
В пространстве прямая может лежать в плоскости, а может и не лежать в ней. Если прямая не лежит в плоскости, то по аксиоме принадлежности прямой плоскости она не может иметь с этой плоскостью более одной общей точки. Это означает, что плоскость и не лежащая в ней прямая либо имеют ровно одну общую точку (прямая пересекает плоскость), либо не имеют ни одной общей точки (прямая параллельна плоскости).
Определение. Прямая и плоскость, не имеющие общей точки, называются параллельными.
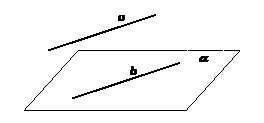
Теорема (признак параллельности прямой и плоскости). Если прямая, не лежащая в плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то эти прямая и плоскость параллельны.
Дано: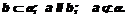 
Доказать: 
Доказательство:
Так как прямая b лежит в плоскости a, то по теореме о двух параллельных прямых, одна из которых пересекает плоскость, прямая а, параллельная прямой b, не может пересекать плоскость. Так как прямая а не лежит в плоскости a, то прямая а параллельна плоскости a.
Из этой теоремы вытекает факт существования и способ построения прямой, параллельной данной плоскости и проходящей через данную точку.
Конус и его свойства. Площадь поверхности и объем конуса.
Пусть в некоторой плоскости задана некоторая замкнутая линия F, а вне этой плоскости – точка S. Фигура, образованная всевозможными отрезками SF, соединяющими точку S с точками, принадлежащими линии F, называется конусом с вершиной S и основанием F. Отрезки, соединяющие вершину S конуса с точками основания F конуса, называются образующимиконической поверхности. Высотой конуса называется перпендикуляр, опущенный из вершины конуса на плоскость его основания.
|
|
|
Конус называется прямым круговым, если его основанием является круг, а вершина проецируется в центр этого круга. В таком случае высота является его осью.
Тело, ограниченное конической поверхностью и кругом с границей F, называется конусом.
Конусом (прямым круговым) называется тело, полученное при вращении прямоугольного треугольника вокруг прямой, содержащей катет.
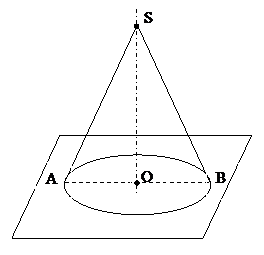Точка S – вершина конуса, круг с центром в точке О - основание конуса, отрезок SА – образующая, отрезок АО – радиус основания, отрезок SО – высота конуса, отрезок АB – диаметр основанияконуса. Треугольник АSВ – осевое сечение конуса.
Свойства прямого кругового конуса.
1. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса. Осевое сечение конуса – равнобедренный треугольник, боковые стороны которого – образующие, а основание – диаметр основания конуса. Все осевые сечения конуса - равные равнобедренные треугольники. ÐASB - угол при вершине осевого сечения конуса.
|
|
|
2. Любое сечение конуса плоскостью, параллельной плоскости осевого сечения конуса, также является треугольником, подобным треугольнику в осевом сечении.
3. Любое сечение конуса плоскостью, перпендикулярной оси конуса, является кругом меньшего по сравнению с основанием радиуса, причем центр этого круга лежит на оси конуса.
4. Любое сечение конуса плоскостью, проходящей через вершину конуса, но не проходящей через его ось, также является равнобедренным треугольником, образующим с плоскостью основания некоторый острый угол.
5. Любое сечение конуса плоскостью, не параллельной плоскости основания и не пересекающей основание,по форме является эллипсом, а в случае, когда плоскость пересекает плоскость основания, - частью эллипса. Поэтому эллипс называют коническим сечением.
6. Сечение, проходящее через ось симметрии конуса, делит его на два равных тела.
7. Плоскость, проходящая через образующую конуса перпендикулярно плоскости осевого сечения, проведенного через эту образующую, называется касательной плоскостью к конусу. Через каждую точку боковой поверхности конуса можно провести лишь одну касательную плоскость к конусу.
|
|
|
Боковой поверхностью прямого кругового конуса называется фигура, состоящая из тех его образующих, которые соединяют граничные точки оснований конуса, т. е. точки двух окружностей, ограничивающих основания цилиндра. Полной поверхностью прямого кругового конуса называется объединение его основания и боковой поверхности.
Если боковую поверхность конуса разрезать по одной из образующих, получится объединение плоских фигур – сектора с радиусом, равным длине образующей, и длиной дуги, равной длине окружности основания, и круга радиуса R, называемое разверткойпрямого кругового конуса.
Теорема о площади боковой поверхности конуса: Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.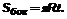 
Доказательство:
Развертка боковой поверхности конуса - сектор круга радиуса ℓ - образующей конуса. Сектор составляет часть круга, определяемую как отношение длины дуги сектора к длине окружности радиуса ℓ.
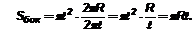
Площадь основания конуса: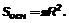 
Площадь полной поверхности конуса: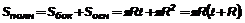 
Объем конуса: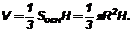 
Билет № 6.
Дата добавления: 2018-04-04; просмотров: 501; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!