Площадью боковой поверхности усеченной пирамиды называется сумма площадей всех ее боковых граней
Теорема о площади боковой поверхности правильной усеченной пирамиды. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований на апофему.
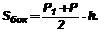
Доказательство: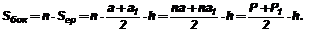 
Теорема об объеме усеченной пирамиды. Объем усеченной пирамиды, у которой площади оснований равны S1 и S2, а высота - Н, вычисляется по формуле: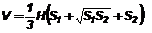 
Доказательство:
Дополним усеченную пирамиду до полной. Тогда объем усеченной пирамиды равен разности объемов полной и дополнительной пирамид.
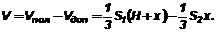
По свойству параллельных сечений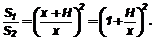 
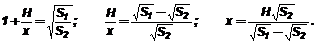
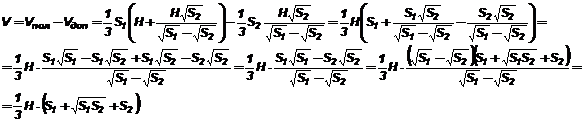
Билет № 2.
Классификация взаимного расположения двух прямых в пространстве. Признак скрещивающихся прямых.
Виды взаимного расположения прямых в пространстве.
Пересекающиеся прямые – прямые, лежащие в одной плоскости и имеющие одну общую точку.
Параллельные прямые – прямые, лежащие в одной плоскости и не имеющие общих точек.
Скрещивающиеся прямые – две прямые, не лежащие в одной плоскости.
Определение: Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. Иначе говоря, скрещивающиеся прямые – это прямые, через которые не проходит ни одна плоскость.
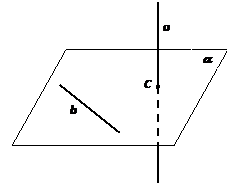Теорема (признак скрещивающихся прямых). Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещиваются.
|
|
|
Дано: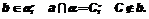 
Доказать: а и b скрещиваются.
Доказательство (метод от противного):
1. Предположим, что прямые а и b не скрещиваются. Тогда они либо пересекаются, либо параллельны. В обоих случаях прямые а и b лежат в одной плоскости – плоскости b.
2. Плоскость b содержит прямую b и точку С – точку пересечения прямой а с плоскостью a. а ∩ a = С.
3. Согласно принятому допущению плоскости a и b совпадают, т. е. прямая а лежит в плоскости a.
4. Это противоречит условию, так как прямая а пересекает плоскость a. Следовательно, прямые а и b не лежат в одной плоскости, а значит, скрещиваются по определению скрещивающихся прямых.
Из доказательства следует, что прямая, пересекающая плоскость в некоторой точке М, скрещивается с любой прямой, лежащей в плоскости и не проходящей через точку М.
Теорема А (признак скрещивающихся прямых). Если четыре точки А, В, С и Е не лежат в одной плоскости, то прямые АВ и СЕ, АС и ВЕ, АЕ и ВС попарно скрещиваются.
Доказательство:
Через любые три точки, согласно аксиоме плоскости, можно провести плоскость, и притом только одну. Проведем плоскость АВС. Тогда согласно условию точка Е не лежит в плоскости АВС. Тогда согласно аксиоме принадлежности прямой плоскости прямая СЕ пересекает плоскость АВС в точке С. Точка С не лежит на прямой АВ, так как в противном случае через точки А, В и С можно провести бесконечное множество плоскостей, а четыре точки А, В, С и Е лежат в одной плоскости.
|
|
|
Дата добавления: 2018-04-04; просмотров: 814; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!