Теорема 1. Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну
Пусть даны прямая а и не принадлежащая ей точка А. Выберем на прямой а две любые точки В и С. Точка А не принадлежит прямой а, следовательно, точки А, В и С не лежат на одной прямой. Согласно аксиоме существования плоскостей через точки А, В и С можно провести единственную плоскость a. 
Прямая а имеет с плоскостью a две общие точки – В и С, Þ согласно аксиоме принадлежности прямой плоскости эта прямая лежит в плоскости a. 
Докажем, что другой плоскости, проходящей через точку А и прямую а (А Ï а), не существует. Предположим, что есть другая плоскость b, проходящая через точку А и прямую а. Тогда плоскости a и b проходят через точки А, В и С, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость a – единственная.
Определение: Две прямые в пространстве называются пересекающимися, если они имеют ровно одну общую точку.
Теорема 2. Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.
Пусть прямые а и b пересекаются в точке С. Выберем на прямой а точку А, отличную от точки С (А Ì а, А ≠ С), а на прямой b точку В, отличную от точки С (В Ì b, В ≠ С). Тогда точка В не лежит на прямой а (В Ë а), следовательно, точки А, В и С не лежат на одной прямой. Согласно аксиоме существования плоскостей через точки А, В и С можно провести единственную плоскость a. 
Прямая а имеет с плоскостью a две общие точки – А и С, Þ согласно аксиоме принадлежности прямой плоскости эта прямая лежит в плоскости a. 
|
|
|
Прямая b имеет с плоскостью a две общие точки – B и С, Þ согласно аксиоме принадлежности прямой плоскости эта прямая лежит в плоскости a. 
Таким образом, плоскость a проходит через прямые а и b и является искомой.
Докажем единственность плоскости a. Допустим, что есть другая плоскость b, отличная от плоскости a и проходящая через прямые а и b. Так как плоскость b проходит через прямую а и не лежащую на ней точку В, то по теореме 1 она совпадает с плоскостью a. Плоскость a – единственная.
Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема 3. Через две параллельные прямые можно провести плоскость, и притом только одну.
Пусть прямые а и b параллельны. Из определения параллельных прямых следует, что через прямые a и b можно провести плоскость. Обозначим ее a и докажем, что она единственна.
Допустим, что существует плоскость b, отличная от плоскости a и содержащая каждую из прямых a и b. Выберем на прямой а точку А, а на прямой b – точки В и С. В силу параллельности прямых a и b точки А, В и С не лежат на одной прямой. Каждая из плоскостей a и b содержит обе прямые a и b, а значит, проходит через точки А, В и С. По аксиоме существования плоскости через эти три точки можно провести только одну плоскость. Следовательно, плоскости a и b совпадают.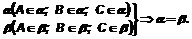 
|
|
|
Способы задания плоскости.
Дата добавления: 2018-04-04; просмотров: 5107; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!