Призма. Виды призм. Боковая и полная площадь поверхности и объем призмы
Призмой называется многогранник, у которого две грани, называемые основаниями призмы, равны и их соответствующие стороны параллельны, а остальные грани – параллелограммы, у каждого из которых две стороны являются соответственными сторонами оснований.
Эти остальные грани называются боковыми гранями призмы, а их стороны, не лежащие на основаниях призмы, - боковыми ребрами призмы. n-угольная призма имеет: n + 2 грани, 3n ребра, 2n вершины. Высотойпризмы называется расстояние между плоскостями ее оснований. Диагональ призмы - отрезок, соединяющий две вершины, не лежащие в одной грани. У n-угольной призмы n(n – 3) диагонали.
Призма называется n-угольной, если ее основание - выпуклый n-угольник. Призма называется прямой, если ее боковые ребра перпендикулярны основанию. В противном случае призма является наклонной. Призма называется правильной, если ее основание - правильный многоугольник, и боковые ребра перпендикулярны основанию.
Сумма площадей всех боковых граней призмы называется площадью ее боковой поверхности. Сумма площадей всех граней призмы называется площадью ее полной поверхности. Поскольку основания призмы - равные многоугольники, то 
Теорема о площади боковой поверхности прямой призмы: Площадь боковой поверхности прямой призмы равна произведению периметра основания призмы на боковое ребро. 
Доказательство: Каждая боковая грань прямой призмы - прямоугольник (боковое ребро перпендикулярно плоскости основания Þ перпендикулярно сторонам основания по свойству прямой, перпендикулярной плоскости). Боковое ребро прямой призмы является ее высотой.
|
|
|
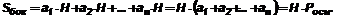
Теорема о площади боковой поверхности наклонной призмы: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения призматической поверхности на боковое ребро. 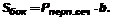
Доказательство: Каждая боковая грань наклонной призмы - параллелограмм. Если рассматривать боковое ребро призмы как основание параллелограмма, то высоты параллелограммов боковых граней, соединенные последовательно, образуют плоский многоугольник, перпендикулярный боковым ребрам по признаку перпендикулярности прямой и плоскости. Этот многоугольник называют перпендикулярным сечением призмы. 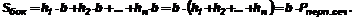
Теорема об объеме прямой призмы: Объем призмы равен произведению площади основания на высоту: 
 Доказательство:
Доказательство:
1. Для прямой треугольной призмы, в основании которой лежит произвольный треугольник. Проведем высоту основания BD, которая разделит треугольник основания на два прямоугольных треугольника: DABD и DCBD. По свойству объемов

2. Для прямой призмы, в основании которой лежит произвольный многоугольник. Разобьем многоугольник основания диагоналями на произвольные треугольники, проведем через диагонали плоскости, перпендикулярные основанию. Призма разобьется на n произвольных треугольных призм, причем по свойству объемов ее объем будет равен сумме объемов полученных треугольных призм:
|
|
|

Теорема об объеме наклонной призмы: Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения: 
Билет № 3.
Дата добавления: 2018-04-04; просмотров: 1449; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
