Определение: Две плоскости, имеющие общую точку, называются пересекающимися плоскостями
Билет № 1.
Основные аксиомы стереометрии и следствия из них. Способы задания плоскости.
Раздел геометрии, в котором изучаются свойства фигур на плоскости (плоских фигур), называется планиметрией. Раздел геометрии, в котором изучаются свойства фигур в пространстве (пространственных фигур), называется стереометрией. Слово «стереометрия» состоит из двух греческих слов «стереос» - телесный, пространственный и «метрео» - измеряю.
Основные фигуры в планиметрии: точка и прямая. Основные фигуры в стереометрии: точка, прямая, плоскость. Плоскость – это множество, элементами которого являются точки и в котором выполняется система аксиом планиметрии, описывающая свойства точек и прямых. Плоскости обозначают строчными греческими буквами: a, b, g… Пространство – это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей.
Система аксиом стереометрии состоит из всех аксиом планиметрии и новой группы аксиом, в которых выражены свойства взаимного расположения точек прямых и плоскостей в пространстве.
Аксиома 1 (аксиома существования плоскости). В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии. Через любые три точки пространства, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
|
|
|
Три точки, принадлежащие одной прямой, называются коллинеарными, а три точки, не принадлежащие одной прямой, называются неколлинеарными. Все точки одной прямой коллинеарны. Любые три неколлинеарные точки определяют плоскость. Плоскость, которая проходит через три точки А, В и С, не лежащие на одной прямой (СÏАВ), обозначают символически АВС; если этой плоскостью является плоскость a, то пишут a = АВС.
Аксиома 2 (аксиома принадлежности точек плоскости). Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Аксиома 3 (аксиома принадлежности прямой плоскости). Если прямая проходит через две точки плоскости, то она лежит в этой плоскости.
Из аксиомы следует: (АÎa, ВÎa) Þ АВ = m; m Ì a. При этом говорят, что плоскость a проходит через прямую m (прямую АВ). В пространстве прямая может и не лежать в данной плоскости, но иметь с этой плоскостью ровно одну общую точку. В таком случае говорят, что прямая пересекает данную плоскость: а ∩ a = {N}.
Определение: Прямая и плоскость, имеющие ровно одну общую точку, называются пересекающимися.
Аксиома 4 (аксиома пересечения плоскостей). Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
|
|
|
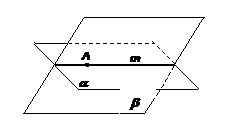Аксиома утверждает, что если две плоскости a и b имеют общую точку А, то они имеют и некоторую общую прямую m, которая проходит через точку А: АÎm. Кроме того из аксиомы следует, что у плоскостей a и b нет общих точек вне их общей прямой m. В таком случае говорят, что плоскости a и b пересекаются по прямой m и записывают: b ∩ a = {m}.
Определение: Две плоскости, имеющие общую точку, называются пересекающимися плоскостями.
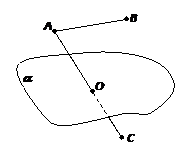Аксиома 5 (аксиома разбиения пространства плоскостью). Любая плоскость a разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что: а) любые две точки, принадлежащие разным множествам, разделены плоскостью a; б) любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью a.
Рассмотрим плоскость a. Она разбивает множество всех не принадлежащих ей точек пространства на два непустых множества P и Q, которые не имеют общих точек. Это разбиение обладает следующим свойством: если две точки (А и В) принадлежат одному и тому же множеству Р, то отрезок АВ не пересекает плоскость a; если же две точки (А и С) принадлежат разным множествам (АÎР, СÎQ), то отрезок АС пересекает плоскость a. Это означает, что точки А и С разделены плоскостью a.
|
|
|
Объединение множества Р и плоскости a (Р È a) называется полупространством, ограниченным плоскостью a. Плоскость a, ограничивающая это полупространство, называется его границей. Объединение множества Q и плоскости a (Q È a) также называется полупространством, ограниченным плоскостью a. Пространство является объединением двух полупространств с общей границей – плоскостью a.
Аксиома 6 (аксиома измерения расстояний). Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, проходящей через эти точки. Согласно аксиоме существования плоскостей в каждой плоскости выполняются аксиомы планиметрии. Следовательно, на каждой плоскости любым двум точкам ставится в соответствие положительное число – расстояние между ними на этой плоскости. Через точки А и В проходят одновременно две различные плоскости a и b; расстояние между точками А и В одно и то же для каждой из двух плоскостей. Расстояние между точками А и В обозначается символом АВ, либо r(А, В), либо │AB │. При выбранной единице измерения расстояние между любыми двумя точками выражается положительным числом, которое показывает, сколько единиц измерения длин и частей этой единицы измерения содержится в данном расстоянии.
Дата добавления: 2018-04-04; просмотров: 1407; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!