ГЛАВА 4. Краткое введение в теорию комплексных чисел
При решении квадратных уравнений вида:
,
появилась необходимость введения нового числа
Если обозначить 
, то мы имеем решение такого уравнения, где корни: 
и 
.
Эти числа, содержащие 
, умноженные на действительное число, называются мнимыми числами. Иначе говоря, наше уравнение имеет два мнимых корня.
Комплексным числом Z называется выражение
,
где a и b - действительные числа, причем если:
1) 
, то 
- мнимое число;
2) 
, то 
- действительное число.
Два комплексных числа 
и 
, отличающиеся только знаком мнимой части называются сопряженными.
Действительное число 
, называется модулем комплексного числа 
. Очевидно, что модули сопряженных комплексных чисел равны.
Всякое комплексное число можно изобразить на плоскости 
в виде точки 
с координатами 
и 
.
|
Рис. 5. Геометрическое изображение комплексного числа |
Точкам, лежащим на оси 
, соответствуют действительные числа 
. Точки, лежащие на оси 
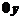, изображают чисто мнимые числа .
Соединив точку с началом координат, получим вектор 0A, который можно считать геометрическим изображением комплексного числа.
Из рисунка видно, что
и, следовательно, комплексное число можно представить в форме
,
которая называется тригонометрической формой записи комплексного числа, где 
-модуль комплексного числа;
-аргумент комплексного числа.
Все основные действия (сложение, умножение, деление, возведение в степень) над комплексными числами производятся по правилам действий над алгебраическим двучленом с учетом того, что
|
|
|
.
Например: 
Если каждому значению комплексного переменного Z из некоторой области комплексных значений соответствует определенное значение другой комплексной величины u то u есть функция комплексного переменного т.е. u=f(Z).
Рассмотрим одну функцию комплексного переменного - показательную функцию
Комплексные значения функции u определяются так:
Если в этой формуле x=0, то получим
Это есть формула Эйлера, выражающая показательную функцию с мнимым показателем через тригонометрические функции.
ГЛАВА 5. Дифференциальные уравнения второго порядка
Определение 15. Уравнение, связывающее независимую переменную x, искомую функцию y и ее производные первого y¢ и второго y² порядков называется уравнением второго порядка.
F(x, y, y¢, y² )=0.
Линейное однородное дифференциальное уравнение
Определение 16. Уравнение вида
y²+ p y¢ +q y = 0, где
p и q постоянные действительные числа, а y - функция переменной x называется линейным однородным дифференциальным уравнением второго порядка.
|
|
|
Пример 3. y²- 5 y¢ +6 y = 0, где p = -5 , q = 6.
Определение 17. Решением линейного однородного дифференциального уравнения второго порядка является функция
y =C1 y1 + C2 y2 ,
при условии, что функции y1 и y2 -
1) частные решения данного дифференциального уравнения
2) y1 ¹ k y2, где k = const, т.е. эти функции не пропорциональны.
Итак, пусть мы имеем однородное уравнение второго порядка
y²+ p y¢ +q y = 0 (1)
Чтобы найти общее решение, как было сказано выше, надо определить два линейно независимых частных решения.
Будем искать частные решения в виде:
y = e kx, где k = const,
тогда : y¢ = k e kx ; y²= k2e kx (2)
Подставим полученные выражения (2) в наше дифференциальное уравнение (1):
k2e kx + p k e kx +q e kx = 0 (3)
Вынесем e kx за скобки:
e kx ( k2 + p k + q ) = 0 (4)
Из (4) следует, что, если e kx не равно 0, то уравнение равно 0 когда:
k2 + p k + q = 0 (5)
Полученное квадратное уравнение (5) называется характеристическим уравнением по отношению к данному дифференциальному уравнению.
Рассматривая пример 3, где y²- 5 y¢ +6 y = 0, характеристическое квадратное уравнение имеет вид: k2 - 5 k + 6 = 0.
Характеристическое квадратное уравнение имеет два корня k1 и k2.
|
|
|
, 
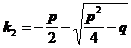
Возможны следующие случаи:
I. k1 и k2 - действительные и притом не равные между собой числа, т.е. k1 ¹ k2.
II. k1 = k2 - действительные равные числа.
III. k1 и k2 - комплексные числа.
IV. k1 и k2 - мнимые числа.
Подводя итог выше изложенному, можно написать алгоритм решения линейного однородного дифференциального уравнения, который сводится к следующему.
Дата добавления: 2018-04-05; просмотров: 389; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!