Механический смысл производной
Рассмотрим прямолинейное движение некоторого твердого тела или материальной точки.
Пусть в некоторый момент времени 
движущаяся точка 
находилась на расстоянии 
от начального положения 
.
Через некоторый промежуток времени 
она переместилась на расстояние 
. Отношение 
= 
- средняя скорость материальной точки . Найдем предел этого отношения, учитывая что 
.
Следовательно, определение мгновенной скорости движения материальной точки сводится к нахождению производной от пути по времени.
Геометрическое значение производной
Пусть у нас есть графически заданная некоторая функция 
.
Рис. 1. Геометрический смысл производной
Если 
, то точка 
, будет перемещаться по кривой, приближаясь к точке .
Следовательно 
, т.е. значение производной при данном значении аргумента 
численно равняется тангенсу угла образованного касательной в данной точке с положительным направлением оси 
.
Таблица основных формул дифференцирования.
Степенная функция
| 
| 
| 
| 
| 
|
Показательная функция
| 
| 
| 
|
Логарифмическая функция
| 
| 
| 
|
Тригонометрическая функция
| 
| 
| 
|
| 
| 
| 
|
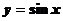
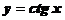
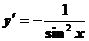
Обратная тригонометрическая функция
| 
| 
| 
|
| 
| 
| 
|
Правила дифференцирования.
Производная от 
Производная суммы (разности) функций
Производная произведения двух функций
|
|
|
Производная частного двух функций
Производная от сложной функции.
Пусть дана функция 
такая, что ее можно представить в виде
и 
, где переменная 
является промежуточным аргументом, тогда 
Производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по x.
Пример1.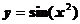 
Пример2. 
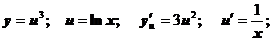
Дифференциал функции.
Пусть есть , дифференцируемая на некотором отрезке 
и пусть у этой функции есть производная
,
тогда можно записать
(1),
где 
- бесконечно малая величина,
так как при 
Умножая все члены равенства (1) на 
имеем:
, где 
- б.м.в. высшего порядка.
Величина 
называется дифференциалом функции 
и обозначается 
.
Геометрическое значение дифференциала.
Пусть дана функция .
Рис.2. Геометрический смысл дифференциала.
.
Очевидно, что дифференциал функции равен приращению ординаты касательной в данной точке.
Производные и дифференциалы различных порядков.
Если есть , тогда 
называется первой производной.
Производная от первой производной называется производной второго порядка и записывается 
.
|
|
|
Производной n-го порядка от функции называется производная (n-1)-го порядка и записывается:
.
Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка.
. 
.
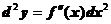Дата добавления: 2018-04-05; просмотров: 356; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!