Примеры для самостоятельной работы
1.  Найти полный дифференциал для следующих функций:
Найти полный дифференциал для следующих функций:
1)  4)
4) 
2)  5)
5) 
3)  6)
6) 
2. Вычислить полное приращение функции z, если дано:
 ,
,  ,
,  ,
, 
Неопределенный интеграл.
Первообразная и неопределенный интеграл
Пусть дана функция  , которая является производной некоторой функции
, которая является производной некоторой функции  , т. е.
, т. е.  .Необходимо найти функцию
.Необходимо найти функцию  . Если такая функция существует, то она есть первообразная от данной функции
. Если такая функция существует, то она есть первообразная от данной функции  .
.
Определение 6. Функция  называется первообразной от функции
называется первообразной от функции  на отрезке
на отрезке  , если во всех точках этого отрезка выполняется равенство
, если во всех точках этого отрезка выполняется равенство  .
.
Пример. Найти первообразную от функции  .
.
Из определения первообразной следует, что функция  является первообразной, так как
является первообразной, так как  .
.
Очевидно, что если для данной функции f(x) существует первообразная, то она не является единственной, так как в качестве первообразных могут быть следующие функции: 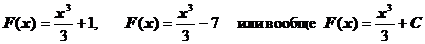 , где С - произвольная постоянная, так как
, где С - произвольная постоянная, так как  .
.
С другой стороны, не сложно доказать, что функциями вида  исчерпываются все первообразные от функции
исчерпываются все первообразные от функции  .
.
Определение 7. Если функция  является первообразной для
является первообразной для  , то выражение
, то выражение  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом  .
.
Таким образом, по определению  , если
, если 
 .При этом функцию
.При этом функцию  называют подынтегральной функцией, а
называют подынтегральной функцией, а  -подынтегральным выражением.
-подынтегральным выражением.
Итак, согласно выше изложенному неопределенный интеграл представляет собой семейство функций  .
.
С геометрической точки зрения неопределенный интеграл представляет совокупность кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т. е. вдоль оси Оy.
Зададимся вопросом: для всякой ли функции  можно найти первообразные, а, значит, и неопределенный интеграл? Оказывается, что не для всякой. Более того, если производная от элементарной функции всегда является элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций.
можно найти первообразные, а, значит, и неопределенный интеграл? Оказывается, что не для всякой. Более того, если производная от элементарной функции всегда является элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций.
Определение 8. Нахождение первообразной для данной функции называется интегрированием
Свойства неопределенного интеграла.
1. Производная от неопределенного интеграла равна подынтегральной функции. 

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению  .
.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная  .
.
4. Неопределенный интеграл от алгебраической суммы нескольких функций равен сумме их интегралов  .
.
5. Постоянный множитель можно выносить за знак интеграла, т.е., если  , то
, то 
 .
.
Таблица интегралов
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6. 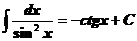 .
.
7.  .
.
8. 
9. 
10.  .
.
11. 
12. 
Примеры нахождения интегралов по формулам:
1. 
2. 
3. 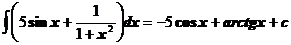
Дата добавления: 2018-04-05; просмотров: 340; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
