Основные элементарные функции
Основными элементарными функциями называются следующие, аналитическим способом заданные функции.
I. Степенная функция 
, где 
- действительное число.
II. Показательная функция 
, где 
- положительное число.
III. Логарифмическая функция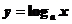 
, где - положительное число, не равное единице.
IV. Тригонометрические функции
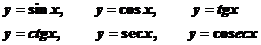
V. Обратные тригонометрические функции
Логарифмы и их свойства
Логарифмом числа N по основанию а называется показатель степени х, в которую нужно возвести а, чтобы получить число N
, при условии, что 
, 
, 
Из определения логарифма следует, что 
, т.е. 
- это равенство является основным логарифмическим тождеством.
Логарифмы по основанию 10 называются десятичными логарифмами. Вместо 
пишут 
.
Логарифмы по основанию e называются натуральными и обозначаются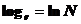 
.
Основные свойства логарифмов.
1) Логарифм единицы при любом основании равен нулю
2) Логарифм произведения равен сумме логарифмов сомножителей.
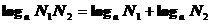
3) Логарифм частного равен разности логарифмов
4) Логарифм степени равен логарифму модуля основания, умноженному на показатель степени. 
5) Логарифм корня равен логарифму модуля подкоренного выражения, деленному на множитель корня. 
6) Зависимость между логарифмами с различными основаниями определяется формулой.
Множитель 
называется модулем перехода от логарифмов при основании a к логарифмам при основании b.
|
|
|
С помощью свойств 2-5 часто удается свести логарифм сложного выражения к результату простых арифметических действий над логарифмами.
Например, 
Такие преобразования логарифма называются логарифмированием. Преобразования обратные логарифмированию называются потенцированием.
ГЛАВА 2. Элементы высшей математики.
Пределы
Пределом функции 
является конечное число А, если при стремлении x®x0 для каждого наперед заданного 
, найдется такое число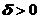 
, что как только 
, то 
.
Функция, имеющая предел, отличается от него на бесконечно малую величину: 
, где e - б.м.в., т.е. 
.
Пример. Рассмотрим функцию 
.
При стремлении 
, функция y стремится к нулю: 
Основные теоремы о пределах.
1. Предел постоянной величины равен этой постоянной величине
.
2. Предел суммы (разности) конечного числа функций равен сумме (разности) пределов этих функций.
.
3. Предел произведения конечного числа функций равен произведению пределов этих функций.
4. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя не равен нулю.
Замечательные пределы
, 
, где 
Примеры вычисления пределов
Пример 1
Однако, не все пределы вычисляются так просто. Чаще вычисление предела сводится к раскрытию неопределенности типа: 
или 
.
|
|
|
Пример 2
.
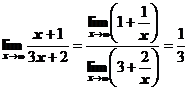Пример 3
.
Производная функции
Пусть мы имеем функцию 
, непрерывную на отрезке 
.
Аргумент 
получил некоторое приращение 
. Тогда и функция получит приращение 
.
Значению аргумента соответствует значение функции .
Значению аргумента 
соответствует значение функции 
.
Следовательно, 
.
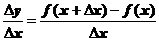
Найдем предел этого отношения при 
. Если этот предел существует, то он называется производной данной функции.
Определение 3 Производной данной функции по аргументу называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента произвольным образом стремится к нулю.
Производная функции может быть обозначена следующим образом:
; 
; 
; 
.
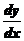Определение 4 Операция нахождения производной от функции называется дифференцированием.
Дата добавления: 2018-04-05; просмотров: 330; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!