Решение биологических задач с применением дифференцирования
Задача 1. Исследования показали, что рост колонии микроорганизмов подчиняется закону 
, где N – численность микроорганизмов (в тыс.), t –время (дни).
а) Рассчитать численность популяции через 7 дней от посева.
б) Будет ли в этот период численность колонии увеличиваться или уменьшаться?
Решение
а) 
б) 
Ответ. Численность колонии будет увеличиваться.
Задача 2. Вода в озере периодически тестируется для контроля содержания болезнетворных бактерий. Через t дней после тестирования концентрация бактерий определяется соотношением
.
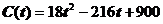
Когда в озере наступит минимальная концентрация бактерий и можно будет в нем купаться?
Решение Функция достигает max или min, когда ее производная равна нулю.
, 
Определим max или min будет через 6 дней. Для этого возьмем вторую производную.
Ответ: Через 6 дней будет минимальная концентрация бактерий.
Функция нескольких переменных.
Рассматривая функции одного переменного, мы не сказали, что при изучении многих явлений приходится встречаться с функциями двух и более переменных. Например, площадь прямоугольника 
, где каждой паре значений x и y соответствует одно определенное значение S. Следовательно, функция S является функцией двух аргументов или функцией двух переменных.
Функция 
,где каждому изменению n независимых аргументов соответствует одно значение функции называется функцией n переменных.
|
|
|
Частные производные.
Пусть z является функцией двух переменных: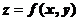 
. Если один из аргументов, например, x изменяется на 
, а остальные аргументы остаются неизменными, то мы имеем частное приращение.
.
Также определяем частное приращение при изменении аргумента y при не изменяющемся аргументе x.
.
Определение 5. Частной производной функции z по аргументу x называется предел отношения частного приращения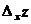 
к приращению при стремлении 
.
Частная производная может обозначаться:
Следовательно, согласно определению имеем две частные производные.
.
Если мы имеем некоторую функцию n независимых переменных, то и частных производных в общем случае будем иметь n.
Пример: 
, т. е. Мы имеем функцию четырех переменных 
. Найдем все частные производные этой функции.
.
Полное приращение и полный дифференциал.
Пусть дана функция 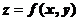. Полное приращение имеет вид:
.
Полным дифференциалом данной функции называется выражение
,
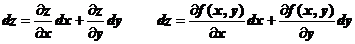где dx и dy –дифференциалы независимых переменных.
Понятие полного дифференциала может быть распространено на функцию любого числа независимых переменных.
Если дифференциалы независимых переменных достаточно малы, то можно считать, что полный дифференциал функции равен приближенно приращению функции: 
. Зная также, что 
и 
, можно записать формулу для полного приращения: 
.
|
|
|
Дата добавления: 2018-04-05; просмотров: 1152; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!