Интегрирование методом замены переменного или способом подстановки
Пусть требуется найти интеграл 
, причем непосредственно подобрать первообразную для 
мы не можем, но известно, что она существует.
Сделаем замену переменной в подынтегральном выражении, положив
, где 
-непрерывная функция. Тогда 
. Следовательно, в этом случае имеет место равенство:
После интегрирования в правой части равенства вместо t необходимо подставить его выражение через x
Приведем несколько примеров на интегрирование с помощью замены переменных:
Пример1. 
, так как мы сделали замену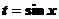 
, тогда 
Таким образом, интегрирование свелось к нахождению табличного интеграла
Пример2.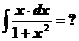 
Полагаем 
; тогда 
и 
Пример3. 
Полагаем 
; тогда 
, 
Интегрирование по частям
Если u и v – две дифференцируемые функции от x, то дифференциал их произведения вычисляется по известной формуле
Проинтегрируем это выражение
или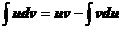 
Последнее выражение называется формулой интегрирования по частям.
Пример 
Положим u=x, dv=sinxdx, тогда du=dx, v=-cosx.
Определенный интеграл
Мощным средством в математике, физике, механике и других дисциплинах является определенный интеграл -одно из основных понятий математического анализа. Вычисление площадей, ограниченных кривыми, объемов, работы, скорости и т. д. Сводится к вычислению определенного интеграла.
Пусть на отрезке 
задана непрерывная функция 
.Разделим отрезок на n интервалов. В каждом интервале возьмем по точке, которые обозначим 
… 
.В каждой из этих точек вычислим значение функции 
…, 
. Составим сумму:
|
|
|
.
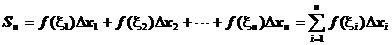Эта сумма называется интегральной для функции 
на отрезке .
Предположим, что при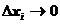 
интегральная сумма стремиться к некоторому пределу 
, тогда этот предел будем считать определенным интегралом.
 |
Определение 9. Если при любых разбиениях отрезка
и при любом выборе точек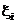 
интегральная сумма при 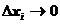стремиться к одному и тому же пределу S, то этот предел называется определенным интегралом от функции f(x) на отрезке и обозначается: 
Таким образом, по определению:
Число a называется нижним пределом интегрирования, число b – верхним пределом интегрирования.
Основные свойства определенного интеграла.
1) Постоянный множитель можно выносить за знак определенного интеграла
2) Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов этих функций. 
3) Если точка с находится внутри отрезка , то справедливо равенство:
Вычисление определенного интеграла. Формула Ньютона – Лейбница.
Формула Ньютона – Лейбница дает практический, удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции.
|
|
|
Если F(x) есть первообразная от непрерывной функции f(x) ,то справедлива формула:
Разность можно заменить знаком двойной подстановки, который в литературе встречается в двух видах:
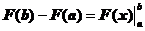
Примеры вычисления определенного интеграла
Пример 1
Пример 2
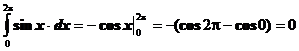
Пример 3
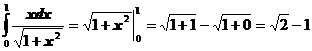
Дата добавления: 2018-04-05; просмотров: 527; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!