Дробный факторный эксперимент

С увеличением числа факторов резко возрастает количество опытов ПФЭ. Так при 5-и факторах оно равно 32, при 6-и — 64 и т.д. Выполнить такое количество опытов технически сложно. Кроме того, значительно возрастает число степеней свободы при нахождении коэффициентов полинома. Для ПФЭ 2⁵ необходимо найти 6 коэффициентов, следовательно число степеней свободы, т.е. количество избыточных значений Y_u, составит 32 – 6 = 24.

Существует методика уменьшения числа опытов — дробный факторный эксперимент, план которого представляет собой некоторую часть (½, ¼ и т.д.) плана ПФЭ.

План ДФЭ строится следующим образом. Способом чередования знаков заполняются столбцы не для всех, а только для части факторов. Поскольку в линейной модели (5.1) эффекты взаимодействия между несколькими факто­рами не учитываются, уровни оставшихся факторов получаются с использо­ва­нием некоторых генерирующих соотношений между факторами первой груп­пы.

Генерирующее соотношение — произведение факторов, заменяемое в матрице новой независимой переменной. Например, для случая четырех факто­ров, когда факторы х₁, х₂ и х₃ являются свободными, для получения значений фактора х₄ можем использовать такие генерирующие соотношения:

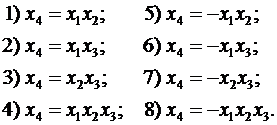                                                      (5.11)

Выбор некоторого генерирующего соотношения означает, что при прове­де­нии эксперимента мы пренебрегаем эффектом взаимодействия соответству­ющих факторов. Так, выбрав вариант 4, мы исключим из анализа эффект взаимо­действия трех факторов х₁, х₂ и х₃. В таком случае матрица ДФЭ 2^4-1 будет иметь вид, представленный в табл. 5.2

Таблица 5.2 — Матрица планирования ДФЭ 2^4-1

Номер опыта	Факторы					Параметр
	x0	x1	x2	x3	x4 = x1x2x3
1	+1	+1	–1	–1	+1	Y1
2	+1	–1	–1	–1	–1	Y2
3	+1	+1	+1	–1	–1	Y3
4	+1	–1	+1	–1	+1	Y4
5	+1	+1	–1	+1	–1	Y5
6	+1	–1	–1	+1	+1	Y6
7	+1	+1	+1	+1	+1	Y7
8	+1	–1	+1	+1	–1	Y8

Дробный факторный эксперимент позволяет сократить число опытов, однако теперь оценки коэффициентов не будут раздельными, как в ПФЭ. Как видно из матрицы планирования, оценка коэффициента b₄ будет смешана с оценкой b₁₂₃, который мы исключили из рассмотрения. Однако, смешанными оказываются и другие коэффициенты.

Умножив генерирующее соотношение на фактор, стоящий слева, полу­чим 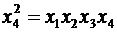, или, учитывая, что ,

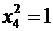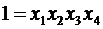                                             .                                           (5.12)

Это т.н. определяющий контраст — соотношение между факторами, определяющее разрешающую способность матрицы. Умножив левую и правую части определяющего контраста на фактор x_i, получим ответ, какой эффект смешан. Например, для фактора x₁

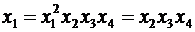                                   ,                                  (5.13)

т.е. оценка коэффициента b₁ смешана с оценкой b₂₃₄. Аналогично получим

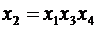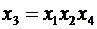                             и ,                           (5.14)

Смешанными оказываются и оценки коэффициентов взаимодействия двух факторов:

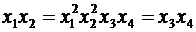                                   ,                                  (5.15)

т.е. смешаны оценки коэффициентов b₁₂ и b₃₄.

Разрешающая способность матрицы тем выше, чем выше порядок генерирующего соотношения, поскольку, например, эффект взаимодействия трех факторов обычно меньше, чем двух, и пренебрежение этим эффектом приводит к меньшей ошибке.

Планирование отсеивающих экспериментов

Для разделения факторов на значимые и незначимые часто недоста­точно изучения и анализа априорной информации об объекте. Необходимы специаль­ные исследования — отсеивающие эксперименты.

Их проводят на начальной стадии до планирования и постановки ос­новного эксперимента. Планирование отсеивающих экспериментов стремятся свести к минимальному числу опытов.

Для выделения значимых факторов используются: метод экспертных оценок, планы Планкета – Бермана, метод случайного баланса, планы дробного факторного эксперимента.

Для отсеивания факторов достаточным является анализ линейной мо­дели. Число коэффициентов такой модели l = k+1, где k — число факторов. В зависимости от соотношения между числом опытов n и определяемым числом коэффициентов планы де­лятся на ненасыщенные (n > l), насыщенные (n = l) и сверх­насыщенные (n < l).

Матрица планирования дробнофакторного эксперимента составляется в соответствии с изложенным ранее.

Для оценки воспроизводимо­сти проводят параллель­ные опыты по всем строкам матрицы или, что делается чаще, ограничи­ваются опытами в одной точке факторного пространства. Обычно в качест­ве таковой принимают центр плана (нулевые уровни всех факторов).

Коэффициенты уравнения регрессии определяются методом наименьших квадратов. Значимость коэффициентов, определяющая степень значимости соответствующих факторов, оценивается с использованием критерия Стьюден­та.

Методы оценки воспроизводимости опытов, регрессионного анализа (метод наименьших квадратов) и оценки значимости коэффициентов уравнения регрессии приведены ниже.

Планы второго порядка

Если описать процессы в объекте ли­нейным уравнением не удается, то переходят к планам второго порядка.

Для получения коэффициентов регрессии в этом случае варьирования факторами на двух уровнях недостаточно. При небольшом количестве факторов можно варьировать каждый фактор на трех уровнях — верхнем, нижнем и нулевом. Полнофакторный эксперимент в таком случае обозначается как 3^k. Однако, переход к полному факторному эксперименту на трех уровнях связан с постановкой большого числа опы­тов. Так, для четырех факторов ПФЭ 3⁴ требует 3⁴ = 81 опыт, а ПФЭ 3⁵ — 243.

Бокс и Уилсон обосновали возможность использования схем, в которых план типа 2^k, используемый в качестве «ядра», дополняется «звездными»точками (по две на каж­дый фактор), а также нулевой точкой в центре плана. На рис. 5.3 показано распо­ложение точек факторного пространства такого плана для двух входных переменных. «Звездные» точки отстоят от центра плана на расстоянии α, называемом «плечом». Оптимальная величина «плеча» зависит от числа свободных факторов, табл. 5.3.

Общее количество опытов с использо­ванием звездных точек составляет

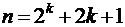                                          ,                                         (5.16)

 Пример построения матрицы второго порядка для двухфакторного эксперимента показан в табл. 5.4.

 

Таблица 5.3 — Данные к построению матриц планов второго порядка

Количество факторов k	2	3	4	5	4	5
Количество опытов ПФЭ 3k	9	27	81	243	81	243
Тип ядра	ПФЭ 2k				ДФЭ 2k-1
Количество опытов «ядра» (2k)	4	8	16	32	8	16
Общее количество опытов (2k+2k+1)	9	15	25	43	17	27
Величина «плеча» α	1,414	1,682	2,000	2,378	1,682	2,000

Таблица 5.4 — Матрица плана второго порядка для трех факторов

Номер опыта	Факторы				Параметр
	x0	x1	x2	x3
1	+1	+1	–1	–1	Y1
2	+1	–1	–1	–1	Y2
3	+1	+1	+1	–1	Y3
4	+1	–1	+1	–1	Y4
5	+1	+1	–1	+1	Y5
6	+1	–1	–1	+1	Y6
7	+1	+1	+1	+1	Y7
8	+1	–1	+1	+1	Y8
9	+1	–1,682	0	0	Y9
10	+1	1,682	0	0	Y10
11	+1	0	–1,682	0	Y11
12	+1	0	1,682	0	Y12
13	+1	0	0	–1,682	Y13
14	+1	0	0	1,682	Y14
15	+1	0	0	0	Y15

 

Как видно из табл. 5.3. для k = 2 количество опытных точек ПФЭ 3^k и с использованием «звездных» точек одинаковы. С увеличением числа факторов разница в числе опытов ПФЭ и плана «звездных» точек становится весьма сущест­венной. Наибольшая экономия количества опытов может быть достигну­та при использовании в качестве ядра дробного факторного эксперимента.

Экстремальный эксперимент.

 Целью исследования часто является поиск оптимальных условий функ­ци­они­рования объекта. В большинстве случаев необходимо найти сочетание факторов, соответствующее экстремаль­ному (наибольшему или наименьшему) значению параметра. В случае двух факторов функция отклика Y = f (X₁, X₂) может быть представлена графически поверхностью, рис. 5.2 а. В точке M функция отклика достигает оптимального значения Y_опт, которому соответствует сочетание факторов (X_1опт, X_2опт). Проекции сечений поверхности отклика горизонтальными плоскостями на плоскость X₁ОX₂ образуют линии равного отклика.

В случае, если удается описать процесс уравнением второго порядка, точку экстремума можно установить, используя методы мате­мати­ческого анализа. При значительной нелинейности поверхности отклика этого сде­лать нельзя. В последнем случае ставят экстремальный эксперимент. Раз­работано несколько методов его проведения.

Классический метод для поиска экстремума заключается в следующем:

1) Фиксируя значения всех факторов, кроме одного, проводят серию опытов, варьируя выбранный фактор в пределах области его определения с некоторым шагом, рис 5.2 б.

2) Фиксируют выбранный фактор на том уровне, при котором получено максимальное значение функции отклика, после чего проводят следующую серию опытов, варьируя аналогичным образом следующий фактор.

3) Проведя серии опытов для всех факторов, получают точку M′′, прибли­жен­ную к оптимуму.

4) Если приближение к оптимуму недостаточно, проводят дополнитель­ные серии опытов по изложенной методике, но факторы варьируются в меньшей области и с меньшим шагом. Это позволяет получить более точное приближение к точке оптимума.

Использование классического метода требует проведения весьма боль­шого количества опытов, которое растет с увеличением числа факторов. Значительно экономичнее метод «кру­того восхождения»:

1) В области факторного пространства с центром в точке (X′₁, X′₂), кото­рую исследователь счи­тает близкой к оптимуму, ставят ПФЭ, (для большого числа факторов — ДФЭ), рис 5.2 в. Находят уравнение регрессии в виде полинома первой степени и проверяют его адекватность.

2) По уравнению регрессии определяют градиент изменения параметра. Градиентом называется вектор, направленный в сторону наиболее интенсив­ного, «крутого» возрастания значения функции.

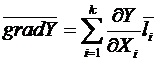                                                                              (5.17)

где 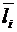 — единичный вектор в направлении координаты X_i факторного про­стран­ства.

Поскольку функция отклика аппроксимирована полиномом первой степени вида (5.1), нетрудно видеть, что частные производные Y по факторам будут равны соответствующим коэффициентам:

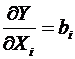                  или 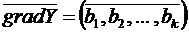                (5.18)

3) Ставят ряд опытов в точках, лежащих на градиенте. Для этого выбирается базовый фактор, который оказывает наибольшее воздействие на параметр, т.е. для которого произведение b_i ΔX_i является наибольшим; здесь ΔX_i — интервал варьирования i-го фактора.

Для базового фактора выбирают шаг смещения h_б. Эта процедура не является формализованной. Здесь многое зависит от опыта экспериментатора, а также априорной информации об объекте исследования.

После выбора шага h_б определяют смещение для других фак­торов:

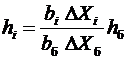                                          .                                         (5.18)

Проводят серию опытов, варьируя все факторы с шагами h_i, при этом опытные точки будут лежать на градиенте. По данным опытов устанавливают положение частного экстремума в данном направлении.

4) В точке частного экстремума ставят новый факторный экспери­мент. Находят уравнение регрессии. Проверяют его адекватность. Ищут направление нового градиента и осуществляют «крутое вос­хождение» по нему в соответ­ст­вии с изложенным ранее.

Поиск прекращается, когда линейная модель оказывается неадек­ватной. Это означает, что достигнута область оптимума. В ней ставят эксперимент второго порядка, по которому уточняют положение оптимума, или просто принимают наилучший из полученных результатов.

 

---

Дата добавления: 2018-04-05; просмотров: 1414; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!