Погрешности косвенных измерений

⇐ ПредыдущаяСтр 14 из 17Следующая ⇒

Часто интересующая нас величина непосредственно не может быть измерена, а определяется как функция других величин, которые находятся опытным путем. Например, расход воздуха в прямоугольном канале

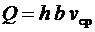, (6.26)

где h и b — высота и ширина канала; v_ср — средняя скорость воздуха. Для определения расхода измеряют ширину, высоту канала и среднюю скорость воздуха. При измерениях этих величин допускаются погрешности. Оценка их может быть выполнена по рассмотренной методике.

Погрешность определяемой величины зависит от погрешностей измеряемых величин и от вида функциональной связи между ними. Предположим, что величина, погрешность которой необходимо определить, является произвольной функцией k измеряемых переменных

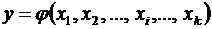, (6.27)

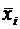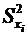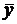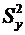Поставив ряд параллельных опытов, найдем оценки и математического ожидания m_xi и дисперсии D_xi для каждой i-й величины. Необходимо определить оценки и математического ожидания m_y и дисперсии D_y для искомой величины.

Распространив свойство (6.17) математического ожидания на его оценку, можем утверждать, что

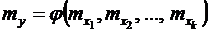и 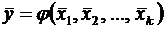. (6.28)

Представим случайные величины x_i в виде 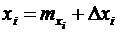, где Δx_i — отклонение величины от ее математического ожидания.

Если функция φ непрерывна и во всех точках интересующего нас интервала имеет производные, то ее, можно разложить в ряд Тейлора. Выполним эту операцию и оставим в ряде только линейные члены:

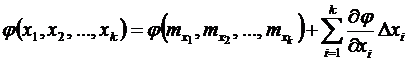С учетом (6.26) и (6.27)

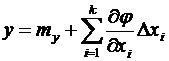или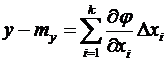

Возведем правую и левую части последнего равенства в квадрат и найдем математические ожидания левой и правой частей:

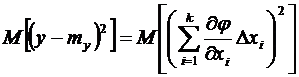
Левая часть равенства есть дисперсия y (6.19). Раскрыв скобки в правой части, получим

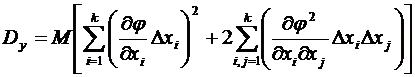или, с учетом свойств (6.15) и (6.16) математического ожидания

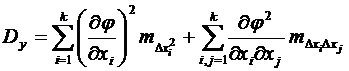Поскольку математическое ожидание квадрата отклонения случайной величины от ее математического ожидания есть дисперсия, а математическое ожидание произведения отклонений двух величин есть их корреляция, для независимых случайных величин равная нулю,

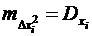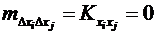и , получим

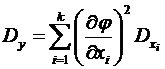. (6.29)

Заменив дисперсии x_i их оценками по выборке 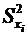, получим зависимость для определения оценки дисперсии величины y:

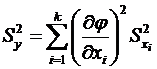. (6.30)

Например, для случая (6.25) 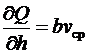, 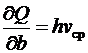и 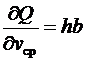. Тогда

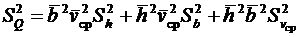В случае, если точность измерения параметров h и b значительно выше, чем точность измерения v_ср, погрешностями этих величин можем пренебречь. Тогда .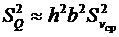

Интервальные оценки измеряемых величин и их погрешностей

В п. 6.3 значение измеряемой величины оценивалось одним числом — выборочным средним. Такая оценка называется точечной. Так как среднее определяется по данным выборки, которая сама является случайной, то случайной будет и оценка. При проведении новой серии опытов на том же объекте будут получены новые результаты, которые будут отличаться от предыдущих. При использовании точечных оценок остаются неизвестными вероятность и точность результатов обработки.

Перечисленных недостатков лишены интервальные оценки. В основе интервальных оценок лежит понятие доверительного интервала.

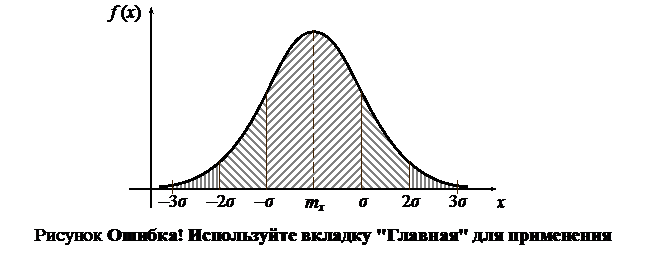
Доверительным называется такой интервал [m_x–Δx_п; m_x+Δx_п], вероят-ность попадания в который реализации случайной величины не ниже заданной P. Величина P называется доверительной вероятностью, а Δx_п — предельной погрешностью. Величина α = 1 – P, равная вероятности ошибки, называется уровнем значимости или риском. Если известен интегральный или дифференциальный закон распределения вероятностей случайной величины, то

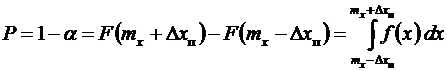. (6.31)

Рассмотрим случайную величину, распределение вероятностей которой подчиняется нормальному закону. При Δx_п= σ_x (интервал m_x ± σ_x) доверительная вероятность P = 0,683, а риск попадания единичного измерения за его пределы α = 0,317, рис. 6.4. Такой риск слишком велик для большинства научных и технических применений. Интервальные оценки выполняют со значительно большей вероятностью.

Вероятность попадания измерения в интервал m_x ± 2σ_xсоставляет 0,955. Риск α = 0,045 уже приемлем. Такой интервал широко используется в инженерной практике. Для интервала m_x ± 3σ_xриск составляет 0,0027, т.е. весьма мал. Интервалы m_x ± 3σ_xиспользуются в очень ответственных расчетах.

Закон распределения вероятностей величины, измеряемой в ходе опыта, обычно неизвестен. В таком случае существует два способа определения доверительного интервала.

1. Определение доверительного интервала по классу точности прибора. Класс точности прибора это выраженная в процентах относительная предельная погрешность измерения величины, равной пределу измерения прибора.

Например, если манометр с максимальным значением по шкале 100 кгс/см² имеет точность ε = 1% то его абсолютная предельная погрешность Δx_п = 100·0,01 = 1 кгс/см². В настоящее время в измерительной технике в большинстве отраслей промышленности под предельной погрешностью прибора понимается величина, равная двум среднеквадратичным отклонениям, т.е. Δx_п= 2σ_x, что соответствует доверительной вероятности P = 0,955 и риску α = 0,045.

Таким образом, доверительный интервал для результата измерения величины x составит x ± Δx_п.

2. Определение доверительного интервала по результатам нескольких параллельных опытов. При наличии выборки из n результатов измерений величины x доверительный интервал составит

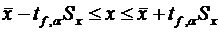, (6.32)

где t_f,α — значение критерия Стьюдента при уровне значимости α и числе степеней свободы f. Число степеней свободы равно разности объема выборки и числа наложенных связей. В данном случае наложена одна связь — определено среднеквадратическое отклонение, поэтому f = n – 1.

Значения критерия Стьюдента при уровне значимости α = 5% приведены в табл. 6.1. Заметно, что с увеличением размера выборки доверительный интервал сужается, т.е. повышается точность определения искомой величины.

Таблица 6.1 – Значения критерия Стьюдента при уровне значимости α = 0,05

f	1	2	3	4	5	6	8	10	20	30	60
t_f,α	12,706	4,303	3,182	2,776	2,571	2,447	2,306	2,228	2,086	2,042	2,00

Дата добавления: 2018-04-05; просмотров: 542; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 8 9 10 11 12 131415 16 17 Следующая ⇒

Мы поможем в написании ваших работ!