Статистическая обработка экспериментальных данных

Виды погрешностей экспериментов

На результаты эксперимента оказывают влияние не только контролируемые факторы, но и неконтролируемые — возмущающие факторы: погрешность измерительных приборов, неточность настройки системы, влияние неучтенных внешних и внутренних факторов и т.д. Воздействие этих факторов приводит к тому, что измеренные в результате опыта величины по своему характеру являются случайными и содержат погрешность.

Погрешность эксперимента — это разность между данными измерения и истинным значением контролируемой величины.

Абсолютная погрешность — разность между истинным значением контролируемой величины и измеренным ее значением:

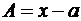, (6.1)

где x – результат измерения; a – истинное значение величины.

Относительная погрешность — отношение абсолютной погрешности к истинному значению величины, выраженное в долях или процентах:

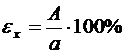. (6.2)

Погрешности делятся на систематические и случайные.

Систематические погрешностивызываются причинами, действующими постоянно и однонаправлено при многократном измерении данной величины. Природа систематических погрешностей обусловлена систематическими погрешностями приборов, неправильной их установкой, неправильным измерением исходных данных и погрешностей в определении расчетных коэффициентов, неучтенными факторами, влияющими на показания приборов. Систематические погрешности должны быть выявлены и устранены до постановки основного эксперимента, поскольку методами статистической обработки выявить и устранить такие погрешности весьма сложно.

Случайные погрешности являются следствием возмущений, действующих при измерении непредсказуемо в сторону уменьшения или увеличения результатов. Они обусловлены нечувствительностью средств измерения, погрешностями наблюдения, округлениями при обработке, случайными колебаниями режима работы исследуемой системы. Случайные погрешности легко устраняются путем проведения серий параллельных опытов с последующей статистической обработкой их результатов.

Законы распределения вероятностей случайных величин

Поскольку в подавляющем большинстве случаев при проведении экспериментальных исследований не удается избежать воздействия возмущающих факторов, параметры ОИ следует рассматривать как случайные величины, а значения этих параметров, измеренные в конкретных опытах — как реализации случайных величин.

Случайные величины бывают дискретными и непрерывными.

Дискретные величины способны принимать лишь ограниченное число значений, известных заранее, например количество успешных опытов или каких-либо объектов, выражаемое целым числом, лежащем в заданном интервале.

Непрерывные величины могут принимать любое значение в некотором интервале. В большинстве случаев результаты опытов являются непрерывными случайными величинами.

Предположим, какая-либо случайная величина измеряется бесконечное число раз. Полученное в результате множество, которое содержит в себе любые значения величины, которые можно получить при реальном эксперименте, называется гипотетической генеральной совокупностью.

Исследователь при постановке опытов делает конечное, обычно небольшое, число измерений. Их можно рассматривать как случайнуювыборку из гипотетической генеральной совокупности. Задача обработки сводится к определению по данным выборки показателей, оценивающих параметры генеральной совокупности.

Для правильного решения этой задачи необходимо знать закон распределения вероятностей случайной величины — зависимость, связывающую значения случайной величины и вероятность появления этих значений.

Для дискретных случайных величин закон распределения вероятностей может быть задан:

1. В табличной форме:

Значение величины X	x₁	x₂	x₃	…	x_i	…	x_n
Вероятность	P₁	P₂	P₃	…	P_i	…	P_n

где x_i – значения случайной величины X (заглавными литерами принято обозначать сами случайные величины, а прописными — их значения); P_i – вероятность, с которой случайная величина примет соответствующее значение.

2. В графической форме — в виде полигона распределения вероятностей, рис. 6.1 а, или гистограммы, рис. 6.1 б. Отличие заключается в том, что в полигоне по оси ординат откладывается вероятность P_i, а в гистограмме — плотность распределения вероятностей — отношение вероятности к величине интервала Δx между значениями:

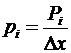(6.3)

Тогда вероятность

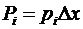есть площадь соответствующего столбца.

3. В аналитической форме — в виде некоторой функции, отражающей зависимость вероятности от значения случайной величины.

Задать закон распределения вероятностей непрерывной случайной величины одним из описанных выше способов невозможно, поскольку непрерывная величина может принимать бесконечное множество значений. Вероятность того, что такая величина примет некоторое заданное значение, всегда равна нулю.

Закон распределения вероятностей непрерывной случайной величины задается в виде функции, равной вероятности того, что случайная величина X будет меньше заданной величины x:

. (6.4)

Такая функция называется интегральной функцией распределения вероятностей случайной величины. Эта функция неубывающая, F(–∞) = 0, F(+∞) = 1. Вид графика функции F(x) показан на рис. 6.2 а.

Интегральная функция распределения вероятностей позволяет определить вероятность попадания значения случайной величины на некоторый интервал [x₁; x₂]:

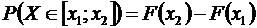. (6.5)

Закон распределения вероятностей непрерывной случайной величины может быть задан также в виде дифференциальной функции, или плотности распределения вероятностей.

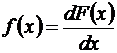. (6.6)

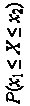
Вид графика функции f(x) показан на рис. 6.2 б. Вероятность попадания значения случайной величины на интервал [x₁; x₂] равна площади фигуры под графиком функции f(x) на этом интервале:

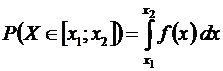. (6.7)

Отсюда следует, что площадь под всей кривой функции f(x) должна быть равна 1, поскольку это вероятность попадания X на интервал (–∞; +∞):

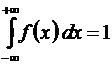. (6.8)

Это свойство плотности распределения вероятностей называется свойством нормирования.

Преимущество дифференциальной функции распределения вероятностей перед интегральной заключается в ее наглядности. Окрестность максимума функции соответствует области наиболее вероятных значений случайной величины.

Для оценки закона распределения вероятностей в реальном эксперименте проводят большое число параллельных опытов. В результате получают выборку реализаций величины X объемом n. Весь диапазон значений величин делят на равные интервалы. Число интервалов рекомендуется принимать

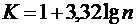(6.9)

Затем подсчитывают количество n_u попаданий значений X в каждый из интервалов. Отношение этой величины к общему числу измерений n

(6.10)

называется относительной частотой попадания и является оценкой вероятности попадания единичных измерений в соответствующий интервал. Оценку плотности вероятности попадания случайной величины в интервал можно получить, разделив на величину интервала:

(6.11)

По полученным результатам строят гистограмму или график распределения плотностей вероятностей, рис. 6.3, по которому можно оценить вид закона распределения плотностей вероятностей для генеральной совокупности. При построении графика условно принимают , где — середина u-гоинтервала.

Для получения аналитического выражения закона распределения вероятностей выполняют аппроксимацию полученных данных зависимостью того или иного вида. Известно несколько видов таких зависимостей, но в большинстве случаев используется нормальный закон распределения вероятностей (закон Гаусса)

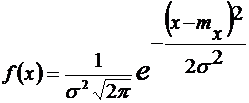, (6.12)

где m_x и σ — параметры нормального закона (математическое ожидание и среднеквадратическое отклонение).

Нормальному закону подчиняются величины, случайный характер которых обусловлен действием множества независимых случайных факторов. Таково большинство погрешностей измерений. Преимуществом нормального закона является простота получения оценок его параметров m_x и σ по данным выборки. Вид графика нормального закона распределения вероятностей показан на рис. 6.2 б. Распределение плотностей вероятностей в выборке, показанное на рис. 6.3, также соответствует нормальному распределению.

Дата добавления: 2018-04-05; просмотров: 801; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒

Мы поможем в написании ваших работ!