Изолированные, открытые , закрытые термодинамические системы. Гомогенные и гетерогенные системы. Экстенсивные и интенсивные свойства системы
Теплота, работа, термодинамическая система, параметры и уравнение состояния?, открытая, закрытая и изолированная системы
Системой называют отдельное тело или группу тел, фактически или мысленно отделенных от окружающей среды.Систему называют термодинамической, если между телами ее составляющими может происходить обмен теплотой, веществом, и если система полностью описывается термодинамическими параметрами (кипящий чайник).
Открытая термодинамическая система – это такая система, которая может обмениваться с окружающей средой энергией и веществом, (например, кипящий чайник).
Закрытой системой называют систему, которая не может обмениваться веществом с окружающей средой, но может обмениваться теплотой и работой. ( плотно закрытая колба с раствором, которая нагревается или охлаждается окружающей средой.)
Изолированной термодинамической системой называют систему, не имеющую обмена веществом и энергией с окружающей средой. Внутри системы может происходить передача теплоты от более нагретой части системы к более холодной, взаимное превращение энергий, выравнивание концентраций, однако внутренняя энергия системы остается постоянной. Примером такой системы является химическая реакция, идущая в термостате.
Гомоге́нная систе́ма — однородная система, химический состав и физические свойства которой во всех частях одинаковы или меняются непрерывно, без скачков (между частями системы нет поверхностей раздела).
|
|
|
Гетероге́нная систе́ма — неоднородная система, состоящая из однородных частей (фаз), разделённых поверхностью раздела. Однородные части (фазы) могут отличаться друг от друга по составу и свойствам.
Интенсивные и экстенсивные свойства системы:
1. Экстенсивное свойство системы прямо пропорционально массе системы и обладает аддитивностью (можно складывать): V, H, Uвн, S, G, F.
2. Интенсивное свойство системы не зависит от массы системы и не обладает свойством аддитивности: Q, A, T, P.
Применение теории активного комплекса к реакциям в растворе
Применение теории активного комплекса к реакциям в растворе.
Теория абсолютных скоростей реакций, строго говоря, применима только для рассмотрения реакций в идеальных газах, когда исходные частицы и активированный комплекс можно рассматривать изолированно от окружающей среды.
В растворе образование активированного комплекса из исходных частиц сопровождается теми или иными изменениями молекулярных взаимодействий реагирующих частиц с молекулами растворителя.
Жидкое состояние вещества является промежуточным между твердым и газообразным. Отличаясь от газа и твердого тела, жидкость имеет черты сходства с каждым из этих состояний.
|
|
|
Применение теории активированного комплекса к кинетике реакций в растворах
Для применения этой теории к жидкости необходимо учесть межмолекулярные взаимодействия исходных частиц и активированного комплекса с молекулами окружающей среды.
Рассмотрим уравнение переходного состояния:
.
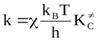Раствор нельзя считать идеальным, так как имеется межмолекулярное взаимодействие, поэтому необходимо вместо Kcввести Ka: 
;
,
,
.
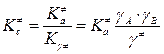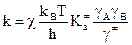При γ = 1 система идеальная.
Если перейти к изобарному потенциалу, то
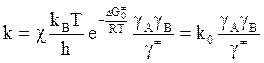,везде - это 1
где 
– изобарный потенциал при активности, равной единице.
,
k0– константа скорости в среде, для которой коэффициенты активности исходных частиц и активированного комплекса приняты равными единице.
Это соотношение называется уравнением Бренстеда-Бьеррума. Данное уравнение в принципе решает вопрос о влиянии среды на скорость элементарной химической реакции, сводя задачу к определению коэффициента активности исходных веществ и активированного комплекса. Однако в то время как существует ряд методов, позволяющих измерить коэффициент активности исходных веществ, величину g¹не удается экспериментально измерить из независимых данных. Поэтому уравнение Бренстеда-Бьеррума имеет лишь теоретическое значение.
|
|
|
Дата добавления: 2018-04-04; просмотров: 3501; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!