Вопрос 2. Частотный критерий устойчивости Найквиста
Критерий Г. Найквиста позволяет по амплитудно-фазовой частотной характеристике разомкнутой системы оценить устойчивость замкнутой системы с отрицательной обратной связью. АФЧХ может быть получена экспериментально или аналитически.
АФЧХ можно построить на комплексной плоскости [+1; j] или в полярной системе координат, если откладывать угол фазы φ(w) и в этом направлении откладывать вектор длиной А(w). Соединив концы векторов получим амплитудно-фазовую характеристику.
Амплитуда передаточной функции разомкнутой системы АРАЗ(w) равна произведению амплитуд отдельных звеньев, а фаза φРАЗ(w) – сумме фаз звеньев:
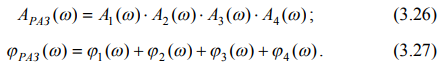
Найти амплитуду А(w) и фазу φ(w) можно по вещественной U(ω) и мнимой V(ω) составляющим частотной передаточной функции W(jω) звена.
Например, для апериодического звена в передаточную функцию вместо оператора p подставляется выражение jω. Затем, чтобы выделить вещественную U(ω) и мнимую V(ω) части, нужно освободиться от мнимости в знаменателе, умножив числитель и знаменатель функции на сопряженный комплекс:
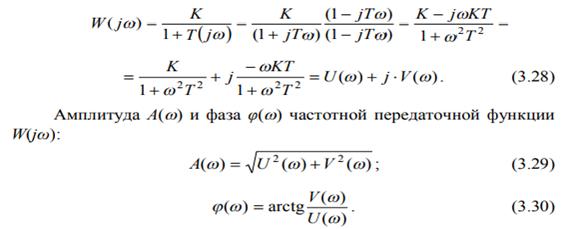
Вещественную UРАЗ(ω) и мнимую VРАЗ(ω) составляющую час- тотной передаточной функции разомкнутой системы WРАЗ(jω) можно определить по амплитуде АРАЗ(w) и фазе φРАЗ(w):
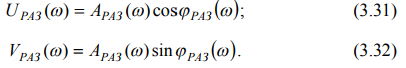
3. Определить сигнал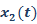 
на выходе системы по известному входному сигналу и передаточной функции системы
. 
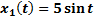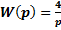
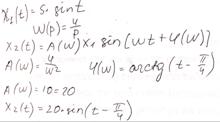
Билет №20
|
|
|
Вопрос 2. Интегрирующие звенья. Изодромное звено.
Интегрирующим звеном называется типовое звено, которое описывается уравнением
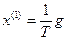(5.27)
или x(1) = kg , (5.28)
где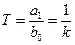 
- «постоянная времени» звена, имеющая размерность времени лишь при одинаковых размерностях величин x и g ;
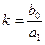- передаточный коэффициент звена, характеризующий отношение скорости изменения выходной величины x(1) к входной величине g .
Иногда уравнение интегрирующего звена записывают в виде
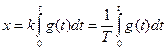, (5.29)
т.е. выходная величина является интегралом от входной величины.
Передаточная функция интегрирующего звена имеет вид
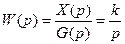(5.30)
или
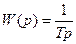. (5.31)
Полагая в выражениях (5.30) и (5.31) p=jw, получим выражение для частотной передаточной функции звена
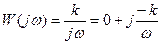. (5.32)
Совершенно очевидно, что вещественная частотная характеристика U(w)=0, а мнимая частотная характеристика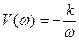 
.
Пользуясь выражением (5.32) и изменяя частоту w от 0 до ¥, построим амплитудно-фазовую характеристику (АФХ). Очевидно, конец вектора W(jw) движется по отрицательной части мнимой оси от -¥ до 0 (рис.5.10,а).
|
Рис.5.10. Частотные характеристики интегрирующего звена:
а - амплитудно-фазовая; б - амплитудная, в - фазовая
Амплитудная и фазовая частотные характеристики определяются соответственно выражениями:
|
|
|
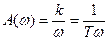(5.33)
и
q(w) = arctg (-¥) = -90° . (5.34)
Из выражения (5.33) следует, что при w®0 A(w)®¥, при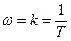 
A(w)=1, а при w®¥ A(w)®0, т.е. амплитуда выходного сигнала x(t) интегрирующего звена при неизменной по величине амплитуде входного сигнала g(t) будет тем меньше, чем больше частота входного сигнала. Из выражения (5.34) следует, что фаза выходного сигнала звена на всех частотах отстает на 90° от фазы входного сигнала. Интегрирующее звено, таким образом, создает отставание (запаздывание) по фазе выходного сигнала относительно входного сигнала независимо от частоты. Графики амплитудной и фазовой частотных характеристик приведены на рис.5.10,б,в.
Как следует из рис.5.10,б и выражения (5.33), характеристика A(w) является разносторонней гиперболой, асимптотами которой служат оси координат.
Логарифмические частотные характеристики интегрирующего звена определяются выражениями:
L(w) = 20 lg A(w) = 20 lg k – 20 lg w (5.35)
и
j(w) = arctg (-¥) = -90° . (5.36)
Изодромная
Особенно широкое распространение получила реальная ГОС(гибкая обратная связь) вокруг интегрирующего звена, которая называется изодромной ОС, в данном случае передаточная функция охваченного звена WЗАМ(p) имеет вид
|
|
|
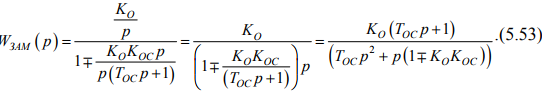
В начале переходного процесса, когда скорость изменения переменных велика, TОС·p>> 1. Поэтому в первой половине переходного процесса инерционная гибкая обратная связь ведет себя как ЖОС, превращая охваченное ею интегрирующее звено в апериодическое. В результате облегчаются условия стабилизации АСР в целом, и возни- 114 кает возможность увеличить коэффициент передачи системы и тем самым повысить быстродействие в начале переходного процесса. Во второй половине переходного процесса постепенно, по мере его замедления сигнал обратной связи ХОС спадает до нуля, в результате чего интегрирующее звено начинает вести себя, как звено без обратной связи, обеспечивая астатизм системы в целом, т. е. устраняя установившееся отклонение.
Рассмотрим интересный случай охвата отрицательной ОС с кор- ректирующим звеном, имеющим передаточную функцию WOС(p), идеального усилительного звена с большим коэффициентом передачи K0 >> 1.
В данном случае передаточная функция звена, замкнутого отрицательной ОС:
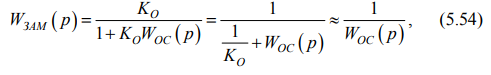
т. к. K0 >> 1, то 1/K0 → 0.
Следовательно, с помощью практически безынерционного усилителя с большим коэффициентом передачи можно получить звено с передаточной функцией, обратной передаточной функции звена обратной связи.
|
|
|
В частности, если WOC(p) = KOC·p, то WЗАМ(p) = 1/ KOC·p , т. е. с помощью дифференцирующего звена в цепи ОС получается интегри- рующее звено. Аналогично с помощью обычного апериодического звена в цепи ОС, получается идеальное ПД звено.
Вопрос 1. Критерий А. Гурвица является достаточным условием для определения устойчивости системы с отрицательной обратной связью и работает с коэффициентами характеристического полинома системы.
Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид (см. п. 2.10)
Тогда передаточная функция системы, охваченной единичной отрицательной обратной связью, (см. п. 2.12) имеет вид
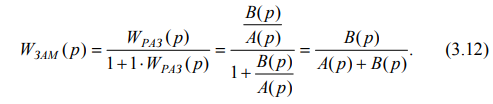
Отсюда следует, что характеристический полином такой замкнутой системы можно определить как сумму полиномов числителя и знаменателя передаточной функции разомкнутой системы WРАЗ(p):
A(p) + B(p) = d0 p n + d1 p n-1 + ….+ dn-1 p + dn. (3.13)
Для определения устойчивости по Гурвицу строится матрица Гурвица, состоящая из коэффициентов характеристического полинома замкнутой системы (3.13).
По главной диагонали матрицы от верхнего левого угла записываются по порядку все коэффициенты характеристического полинома замкнутой системы, начиная с d1 и заканчивая dn.
Затем каждый столбец матрицы дополняется таким образом, чтобы вниз от диагонали номер индекса коэффициента d уменьшался, а вверх – увеличивался. Коэффициенты с индексами меньше 0 и больше, чем n заменяются нулями.
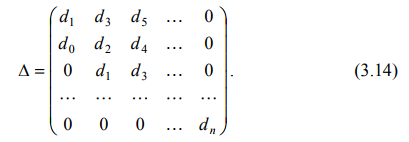
Дата добавления: 2018-04-04; просмотров: 1134; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!