Выпуклость, вогнутость графика функции, точки перегиба
- Признаки выпуклости и вогнутости графика функции
- Признаки существования точки перегиба
- Исследуем характер выпуклости графика вместе
- Исследовать характер выпуклости графика самостоятельно, а затем посмотреть решение
Признаки выпуклости и вогнутости графика функции
Исследование функции на выпуклость и вогнутость может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика. Выпуклость и вогнутость функции имеет место только на определённом интервале, с чем и связаны нижеприведённые определения.
График дифференцируемой функции называется выпуклым в интервале ]a, b[, если в этом интервале он расположен ниже любой своей касательной (рис. 1).
График дифференцируемой функции называется вогнутым в этом интервале он расположен выше любой своей касательной (рис. 2).
Теорема(достаточный признак вогнутости или выпуклости графика). Если для функции f(x) во всех точках интервала ]a, b[
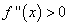
то кривая y = f(x) вогнута в этом интервале; если же
во всех точках интервала ]a, b[, то кривая выпукла в этом интервале.
Признаки существования точки перегиба
Точка графика непрерывной функции, в которой изменяется выпуклость на вогнутость или наоборот, называется точкой перегиба.
Из определения следует, что с одной стороны от точки перегиба кривая расположена под касательной, с другой стороны – над ней, или наоборот. Поэтому точку перегиба на графике принято показывать отрезком касательной, которая в этой точке пересекает кривую (рис. 3).
|
|
|
Теорема (достаточный признак существования точки перегиба). Если в точке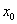 
функция f(x) имеет первую производную 
, а вторая производная 
в этой точке равна нулю или не существует, и кроме того, при переходе через 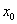меняет знак, то
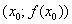
является точкой перегиба графика функции y = f(x).
Исследуем характер выпуклости графика вместе
Таким образом, чтобы исследовать характер выпуклости кривой y = f(x), нужно найти те точки, в которых 
или не существует, а затем, используя достаточный признак, исследовать знаки второй производной слева и справа от каждой возможной точки перегиба (подобно тому, как определялись точки экстремума по первой производной).
Пример 1.Найти точки перегиба и установить характер выпуклости графика функции 
.
Решение. Функция определена при 
. Её производные 
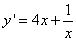и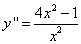 
. Найдём возможные точки перегиба. Полагая 
, получим 
, т. е. 
, полагая 
, получим 
.
Однако точк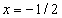и 
и не входят в область определения заданной функции, поэтому она может иметь только одну точку перегиба при 
. Исследуем знаки второй производной в окрестности точки . Взяв в интервале 
точку 
, получим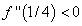 
, а взяв в интервале 
точку 
, имеем 
. Следовательно, слева от кривая выпукла, а справа - вогнута, поэтому при график функции имеет точку перегиба 
.
|
|
|
График этой функции - на рис. снизу.
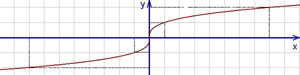
Пример 2. Найти точки перегиба, характер выпуклости и вогнутости и построить график функции 
.
Решение. Функция определена при 
. Её производные 
и 
.Здесь 
, а 
при , причём 
при 
и 
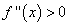при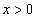 
. Следовательно, слева от кривая вогнута, а справа - выпукла, т.е. 
- точка перегиба графика.
График этой функции - на рис. снизу.
Пример 3.Исследовать на выпуклость, вогнутость и точки перегиба функцию 
.
Решение. Находим вторую производную: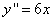 
. Из уравнения 
получаем одну критическую точку: 
. Исследовав знак 
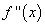в окрестности точки 
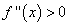получаем: слева от точки (выпуклость), а справа - (вогнутость), т. е. точка является точкой перегиба рассматриваемой функции.
График этой функции - на рис. снизу.
Общее понятие предела
Обобщённое понятие предела: число a есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.
Поясним это на примере, который также проиллюстрируем. А после примера приведём общий алгоритм решения пределов.
|
|
|
В нижнюю часть равнобедренного треугольника вписана окружность. Диаметр этой окружности обозначим как 
. На рисунке диаметр проведён синим цветом. К окружности параллельно основанию первоначального треугольника проведена касательная (она на рисунке серого цвета). В результате получен треугольник, подобный первоначальному. В этот треугольник точно так же вписана окружность. Её диаметр - 
(диаметры на рисунке ограничены касательными). Аналогичные построения продолжаются, пока позволяет высота треугольника. Получена последовательность уменьшающихся окружностей и соответствующая им последовательность длин их диаметров: 
. Эта последовательность длин диаметров даёт пример переменной величины 
, которая с возрастанием номера окружности x неограниченно приближается к нулю. Предел этой последовательности равен нулю: 
.
Запишем приведённый пример на языке формул. Итак, номер окружности возрастает и стремится к бесконечности, то есть 
. Допустим, существует такой равнобедренный треугольник, что длина диаметра каждой вписанной в него окружности расчитывается по формуле
Величина, которую нам требуется найти, будет записана так:
Lim это и есть предел, а под ним указывается переменная, которая стремится к определённому значению – нулю, любому другому числу, бесконечности.
|
|
|
Теперь вычислим предел, присвоив переменной x значение бесконечность (в более строгом определении это называется "доопределить функцию", с этим определением вы можете ознакомиться в последующих частях главы "Предел"). Примем, что конечная величина, поделенная на бесконечность, равна нулю:
С рассмотренной последовательностью окружностей свяжем другую переменную величину 
- последовательность сумм их диаметров:
Рассмотрев рисунок снова, обнаружим, что предел последовательности 
равен h – высоте равнобедренного треугольника. Вообще, предел может быть равен нулю, любому другому числу или бесконечности.
Теперь более строгие определения предела функции, которые Вас могут спросить на экзамене, и для понимания которых потребуется чуть больше внимания.
Предел функции
Предел функции при 
Пусть функция f(x) определена на некотором множестве X и пусть дана точка 
. Возьмём из X последовательность точек, отличных от :
(1)
сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность
(2)
и можно ставить вопрос о существовании её предела.
Определение 1. Число A называется пределом функции f(x) в точке 
(или при ), если для любой сходящейся к последовательности (1) значений аргумента x, отличных от , соответствующая последовательность (2) сходится к числу A.
Символически это записывается так: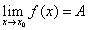 
Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится x.
Пример 1.Найти предел функци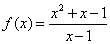и 
при 
.
Решение. Подставляем вместо x значение 0. Получаем:
.
Итак, предел данной функции при равен 1.
Предел функции при 
, при 
и при 
Кроме рассмотренного понятия предела функции при существует также понятие предела функции при стремлении аргумента к бесконечности.
Определение 2. Число A называется пределом функции f(x) при , если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к A.
Символически это записывается так: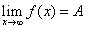 
.
Определение 3. Число A называется пределом функции f(x) при ( ), если для любой бесконечно большой последовательности значений аргумента, элементы 
которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.
Символически это записывается так: 
( 
).
Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо x подставить бесконечность, плюс бесконечность или минус бесконечность.
Пример 2.Найти предел функции 
при 
.
Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:
.
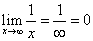Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо xсупербольшое число. При делении получите супермалое число.
Основные теоремы о пределах
Теорема 1.(о единственности предела функции). Функция не может иметь более одного предела.
Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при 
, либо обе не имеют предела в этой точке.
Теорема 2.Если функции f(x) и g(x) имеют пределы в точке 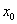, то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
(3)
2) предел произведения функций равен произведению пределов сомножителей, т.е.
(4)
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
(5)
Замечание.Формулы (3) и (4) справедливы для любого конечного числа функций.
Следствие 1.Предел постоянной равен самой постоянной, т.е.
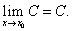
Следствие 2.Постоянный множитель можно выносить за знак предела, т.е.
Пример 3.Найти предел:
Решение.
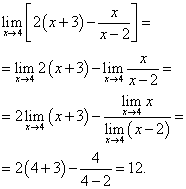
Пример 4.Найти предел:
Решение. Предварительно убедимся, что предел делителя не равен нулю:
Таким образом, формула (5) применима и, значит,
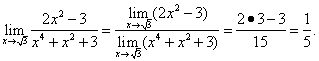
Теорема 3(о пределе сложной функции). Если существует конечный предел
а функция f(u) непрерывна в точке 
, то
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Пример 5.Найти предел:
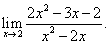
Решение. Теорема о пределе частного здесь неприменима, так как
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
где
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
Дата добавления: 2018-02-28; просмотров: 576; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!