Понятие бесконечно малых функций
Функция 
называется бесконечно малой при 
("икс нулевое" здесь - число или бесконечность), если
Из определения бесконечно малой функции следует, что
1) это понятие относится только к функциям, имеющим пределом нуль. Никакое фиксированное число, кроме нуля, не может быть бесконечно малым. Например, число 
при некоторых условиях можно считать очень малой величиной, но не бесконечно малой, так как это – величина постоянная. Нуль – единственная постоянная, которая является бесконечно малой величиной, поскольку
2) функция может быть бесконечно малой только в определённой точке, а именно - обозначенной выше как "икс нулевое".
Примерами бесконечно малых функций могут служить:
1) длина хорды круга по мере удаления её от центра, так как предел этой функции равен нулю;
2) 
при 
, так как 
3) 
при 
, поскольку 
.
Из теорем о пределах следует, что сумма (разность) и произведение двух бесконечно малых функций есть величина бесконечно малая. Об отношении двух бесконечно малых функций никакого общего заключения сделать нельзя.
Отношение двух бесконечно малых функций в зависимости от характера изменения переменных в числителе и знаменателе может оказаться или числом, или бесконечно малой величиной, или бесконечностью.
Правила сравнения бесконечно малых функций
Пусть при 
функции 
и 
являются бесконечно малыми. Тогда:
1) если 
, то - бесконечно малая функция более высокого порядка, чем (или, что то же самое, имеет более высокий порядок малости, чем при );
|
|
|
2) если 
(A - число), то и - бесконечно малые функции одного порядка;
3) если 
, то и - эквивалентные бесконечно малые функции. Эквивалентность бесконечно малых функций обозначается так: 
.
В некоторых случаях недостаточно знать, что одна из двух бесконечно малых функций является бесконечно малой более высокого порядка, чем другая. Нужно ещё оценить, как высок этот порядок. Для этого существует следующее правило:
4) если 
, то бесконечно малая функция n-го порядка относительно .
Пример 1.Сравнить бесконечно малые функции 
и xпри 
.
Решение. Данные функции при данном условии являются эквивалентными бесконечно малыми, так как 
.
Пример 2.Сравнить бесконечно малые функции 
и при .
Решение. Данные функции при данном условии являются бесконечно малыми одного порядка, так как 
.
Существуют аналогичные правила для сравнения бесконечно малых функций при 
, 
и 
.
К началу страницы
Пройти тест по теме Предел
Нет времени вникать в решение? Можно заказать работу!
Эквивалентные бесконечно малые функции
Итак, как уже замечалось, если , то и - эквивалентные бесконечно малые функции. Эквивалентные - значит, равносильные. Во многих задачах на вычисление пределов можно заменить некоторую бесконечно малую функцию, эквивалентной другой бесконечно малой функции. Это здорово помогает упростить решение задачи и сократить время решения.
|
|
|
Доказана эквивалентность следующих важнейших бесконечно малых функций:
1) 
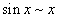
2) 
3) 
4) 
5) 
6) 
( 
)
7) 
8) 
( )
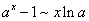9) 
Пример 3.Привести 
к первому замечательному пределу путём использования эквивалентных бесконечно малых функций
Решение. Применяя эквивалентные бесконечно малые функции и , получаем:
.
Что такое производная
- Понятие производной
- Физический смысл производной
- Геометрический смысл производной
Понятие производной
Производная - главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x
Производной функции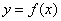 
в точке 
называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
То есть,
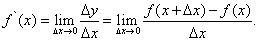(1)
Наиболее употребительны следующие обозначения производной:
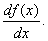
Пример 1.Пользуясь определением производной, найти производную функции
|
|
|
.
Решение. Из определения производной вытекает следующая схема её вычисления.
Дадим аргументу приращение (дельта) и найдём приращение функции:
.
Найдём отношение приращения функции к приращению аргумента:
Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю, то есть искомую производную:
Физический смысл производной
К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в более широком смысле - задачи о мгновенной скорости неравномерного прямолинейного движения точки.
Пусть камешек поднят и затем из состояния покоя отпущен. Путь s, проходимый за время t, является функцией времени, т.е. s = s(t). Если задан закон движения точки, то можно определить среднюю скорость за любой промежуток времени. Пусть в момент времени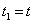 
камешек находился в положении A, а в момент 
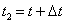- в положении B. За промежуток времени 
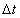(от tдо 
) точка прошла путь 
. Поэтому средняя скорость движения за этот промежуток времени, которую обзначимчерез 
, составляет
.
Однако движение свободно падающего тела явно неравномерное. Скорость v падения постоянно возрастает. То есть, средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути. Такая характеристика тем точнее, чем меньше промежуток времени 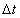. Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени t) называется предел средней скорости при 
:
|
|
|
(при условии, что этот предел существует и конечен).
Таким образом, мгновенная скорость есть предел отношения приращения функции s(t) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.
.
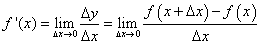Решение обозначенной задачи представляет собой физический смысл производной. Итак, производной функции y=f(x) в точке x называется предел (если он существует и конечен) приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
Пример 2. Найти производную функции
Решение. Из определения производной вытекает следующая схема для её вычисления.
Шаг 1. Дадим аргументу приращение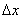 
и найдём
Шаг 2. Найдём приращение функции:
Шаг 3. Найдём отношение приращения функции к приращению аргумента:
Шаг 4. Вычислим предел этого отношения при 
, т.е. производную:
Дата добавления: 2018-02-28; просмотров: 379; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!