Системи і сукупність нерівностей з однією змінною
При розв’язуванні нерівностей іноді необхідно переходити до систем нерівностей або їх сукупностей.
Системою двох нерівностей з однією змінною називається твердження «f1(x)  g1(x) і f2(x)
g1(x) і f2(x)  g2(x)», яке записують за допомогою фігурної дужки:
g2(x)», яке записують за допомогою фігурної дужки:

Так,наприклад запис  означає , що нерівності
означає , що нерівності 
утворюють систему нерівностей.
Число х0 називається розв’язком системи нерівностей, якщо воно є розв’язком кожної із нерівностей.
Тобто розв’язком системи нерівностей є перетин розв’язків нерівностей, які утворюють систему.
Сукупністю двох нерівностей з однією змінною називається твердження «f1(x)  g1(x) або f2(x)
g1(x) або f2(x)  g2(x)», яке записують за допомогою за допомогою квадратної дужки:
g2(x)», яке записують за допомогою за допомогою квадратної дужки:  або у рядок за допомогою знака «;»: «f1(x)
або у рядок за допомогою знака «;»: «f1(x)  g1(x); f2(x)
g1(x); f2(x)  g2(x)»,
g2(x)»,
Число х0 називається розв’язком сукупності, якщо воно є розв’язком хоча б однієї з цих нерівностей.
Тобто розв’язком сукупності нерівностей є об’єднання розв’язків нерівностей, які утворюють сукупність.
Методи розв’язування основних видів нерівностей
Методи розв’язування основних видів нерівностей мають певну аналогію, які вам відомі з 9класу: за допомогою рівносильних перетворень та за допомогою методів інтервалів (  ).
).
Розв'язування нерівностей методом інтервалів спирається на властивості функцій, пов'язані зі зміною знака функції. Будь-яка функція може змінити свій знак тільки в нулях або в точках, де розривається графік функції. Якщо ж на деякому проміжку області визначення графік функції не розривається і функція не дорівнює нулю, то вона не може на цьому проміжку змінити свій знак. Таким чином, якщо позначити нулі функції на її області визначення, то область визначення розіб'ється на проміжки, всередині яких знак функції не змінюється.
|
|
|
 |
| Метод рівносильних перетворень | Метод
інтервалів (  ). ).
| |
|
Урахування ОДЗ початкової нерівності. Збереження на ОДЗ правильної нерівності при прямих і зворотних перетвореннях. | 1.Знайти ОДЗ. 2.Знайти нулі функції: 3. Позначити нулі на ОДЗ і знайти знак функції 4.Записати відповідь, урахо-вуючи знак заданої нерівності. | |
Приклад 1. Розв'язати нерівність  0.
0.
| Метод рівносильних перетворень | Метод
інтервалів ( 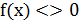 ). ).
| |
ОДЗ х-3  , отже х , отже х 
 0. 0.   х є х є  Відповідь: х є х є
Відповідь: х є х є  . .
| Розв'язати нерівність  0.
Розв’язування
Нехай 0.
Розв’язування
Нехай  .
1.ОДЗ х-3 .
1.ОДЗ х-3  , отже х , отже х  2. Нулі функції:
2. Нулі функції:  )=0 )=0
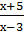 = 0, х+5 = 0, х = -5 (входить до ОДЗ)
3. = 0, х+5 = 0, х = -5 (входить до ОДЗ)
3.
 Відповідь: х є
Відповідь: х є 
|
Основні види нерівностей
Нерівності з однією змінною поділяються на: алгебраїчні та трансцендетні.
|
|
|
Алгебраїчні - це нерівності утворені з чисел і змінних за допомогою дій додавання, віднімання, множення, ділення, піднесення до цілого додатного степеня і добування арифметичного кореня.
Алгебраїчні поділяють на раціональні ( лінійні – 4х+8  , квадратні – 2х2 +3х - 6
, квадратні – 2х2 +3х - 6  0, біквадратні) та ірраціональні (
0, біквадратні) та ірраціональні ( 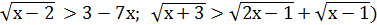 . Раціональні можуть бути як цілими (2х2 +3х - 6
. Раціональні можуть бути як цілими (2х2 +3х - 6  0) так і дробовими (
0) так і дробовими ( 

Всі неалгебраїчні нерівності називаютьсятрансцендентними. До них відносяться: показникові, логарифмічні, тригонометричні. Тому основними (стандартними ) видами нерівностей є:
Ø Лінійні ах+b  ,
,
Ø Квадратні ax2 +bx+ c  ,
,
Ø Степеневі  ,
,
Ø Показникові  ,
,
Ø Логарифмічні  ,
,
Ø тригонометричні sinx  cosx
cosx 
Лінійні нерівності
Лінійною нерівністю з однією змінною називається нерівність виду
ax + b 
Якщо a 
 =
=  (x
(x  )
)  =
=  х
х  (
(  ).
).
Якщо a 
 =
=  (x
(x 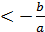 ).
).  =
=  х
х  (
(  ).
).
Приклад 2. Розв’язати нерівність 2х+3 
Розв’язування. 2х+3  =
=  2х- х
2х- х 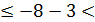 =
=  х
х  =
= 
х є (  .
.
Відповідь: х є (  .
.
Приклад 3. Розв’язати нерівність 
Розв’язування.  =
=  =
= 
 12х+6
12х+6  =
=  х-12х
х-12х  =
=  -11х
-11х 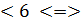 х
х 
Відповідь: 
Квадратні нерівності
Нерівності виду ах2+bx+с 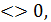 де a,b,с – числа, а
де a,b,с – числа, а  0, х- змінна,
0, х- змінна,  - один із знаків нерівності, називають квадратними.
- один із знаків нерівності, називають квадратними.
|
|
|
Наприклад 7х2+3х-11  , х2 - 8
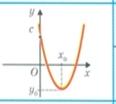
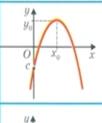
, х2 - 8  -квадратні нерівності. Розв’язування квадратних нерівностей зводять до відшукання проміжків, на яких відповідна квадратична функція у= ах2+bx+с набуває додатних, від’ємних, невід’ємних, значень. Графіком квадратичної функції є парабола, вітки якої направлені: вгору, якщо а
-квадратні нерівності. Розв’язування квадратних нерівностей зводять до відшукання проміжків, на яких відповідна квадратична функція у= ах2+bx+с набуває додатних, від’ємних, невід’ємних, значень. Графіком квадратичної функції є парабола, вітки якої направлені: вгору, якщо а  і вниз, якщо а
і вниз, якщо а  Знайдемо нулі функції ах2+bx+с=0 та проміжки на яких функція. набуває додатних, від’ємних, невід’ємних, недодатних значень
Знайдемо нулі функції ах2+bx+с=0 та проміжки на яких функція. набуває додатних, від’ємних, невід’ємних, недодатних значень
| ах2+bx+с=0 | |||
|
а | 
| D=0 | D 
|
| 
| 
| |
а 
|
| 
| 
|
Показникові нерівності
Нерівність, яка містить змінну величину в показнику степеня, називають показниковою.
Наприклад, 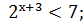
 тощо. Розв’язування показникових нерівностей ґрунтується на властивостях показникової функції:
тощо. Розв’язування показникових нерівностей ґрунтується на властивостях показникової функції:
Ø функція у=  зростає, якщо а
зростає, якщо а 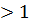 ,
,
Ø функція у=  спадає, якщо
спадає, якщо 
Ø функція у=  набуває лише додатних значень.
набуває лише додатних значень.
Тобто, якщо а 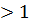 , то
, то 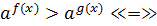 f(x)
f(x) 
якщо 
 f(x)
f(x) 
Логарифмічні нерівності
Нерівність, яка містить змінну величину під знаком логарифма або в його основі, називають логарифмічною. Наприклад,  тощо. Розв’язування логарифмічних нерівностей ґрунтується на властивості монотонності логарифмічної функції: функція у=
тощо. Розв’язування логарифмічних нерівностей ґрунтується на властивості монотонності логарифмічної функції: функція у=  монотонно зростає, якщо а
монотонно зростає, якщо а  , і монотонно спадає, якщо
, і монотонно спадає, якщо  При цьому слід ураховувати, що підлогарифмічний вираз може набувати лише додатних значень. Тобто
При цьому слід ураховувати, що підлогарифмічний вираз може набувати лише додатних значень. Тобто  =
= 
|
|
|
 =
= 
Тригонометричні нерівності
Нерівності, які містить змінну величину під знаком тригонометричної функції, називають тригонометричними. Наприклад, cos x  тощо. Розв’язування тригонометричних нерівностей зводять до розв’язування найпростіших тригонометричних нерівностей. Найпростіші тригонометричні нерівності – це нерівності виду sinx
тощо. Розв’язування тригонометричних нерівностей зводять до розв’язування найпростіших тригонометричних нерівностей. Найпростіші тригонометричні нерівності – це нерівності виду sinx  cosx
cosx  . Розв’язуватинайпростіші тригонометричні нерівності можна графічно або за допомогою одиничного кола.
. Розв’язуватинайпростіші тригонометричні нерівності можна графічно або за допомогою одиничного кола.
За означенням , синусом кута  є ордината точки
є ордината точки  одиничного кола, а косинусом - абсциса точки
одиничного кола, а косинусом - абсциса точки  одиничного кола. Цей факт використовується при розв’язуванні тригонометричних нерівностей виду sinx
одиничного кола. Цей факт використовується при розв’язуванні тригонометричних нерівностей виду sinx  cosx
cosx  за допомогою одиничного кола.
за допомогою одиничного кола.
Розв’язування нерівностей з однією змінною передбачає два кроки:
Ø перетворення нерівностей до стандартної (до одного з основних видів нерівностей з однією змінною);
Ø розв’язування стандартної нерівності.
Перетворення нерівності до стандартної (до одного з основних видів нерівностей з однією змінною) здійснюються за відомими формулами, які завжди можна відновити в пам’яті при допомозі довідників або ж просто їх пам’ятати.
Нерівності з модулем.
Модуль дійсного числа (позначається  )дорівнює самому числу х, якщо х додатнє, дорівнює ( -х), якщо х від’ємне, і модуль нуля дорівнює нулю.
)дорівнює самому числу х, якщо х додатнє, дорівнює ( -х), якщо х від’ємне, і модуль нуля дорівнює нулю.

При розв’язуванні нерівностей, які містять змінну під знаком модуля, використовують наступні рівносильні перетворення:
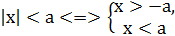


Приклад 4.Розв’язати нерівність 
Розв’язування. 
Відповідь: х є (2;8)
Приклад 5.Розв’язати нерівність 

Розв’язування 

Відповідь: х є (  ; -1)
; -1)  (9; +
(9; +  ).
).
Розв’язуючи нерівність виду  , застосовують піднесення обох частин нерівності до квадрата.
, застосовують піднесення обох частин нерівності до квадрата.
Приклад 6. Розв’язати нерівність  ,
,
Розв’язування. При піднесенні до квадрата обох частин нерівності одержимо:
 ; 4х2 - 4х +1
; 4х2 - 4х +1  9х2 +6х+1; 5х2 +10х
9х2 +6х+1; 5х2 +10х 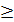 0; х(х+2)
0; х(х+2) 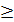 0.
0.
х  [0;
[0;  ).
).
Відповідь: 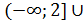 [0;
[0;  ).
).
Перетворення нерівності до одного з основних видів нерівностей з однією змінною є головним кроком при розв’язуванні нерівностей. Повністю алгоритмізувати процес перетворення неможливо, але дуже важливо запам’ятати прийоми, які найбільше використовуються та загальні для всіх типів нерівностей.
3) Розкладання на множники.
Якщо дану нерівність при допомозі перетворень можна звести до виду
f(x)∙g(x)<>0. То дана нерівність буде рівносильна сукупності двох більш простих систем нерівностей 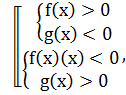 в області визначення нерівності f(x)∙g(x) <>0 або використати метод інтервалів.
в області визначення нерівності f(x)∙g(x) <>0 або використати метод інтервалів.
Приклад 7. Розв’язати нерівність 6  .
.
Розв’язування: 6  . Винесемо за дужки спільний множник 6х . 6
. Винесемо за дужки спільний множник 6х . 6  . Знайдемо корені:
. Знайдемо корені:
 .Звідси маємо х= 0, х = -1, х = -2.Нанесемо на числову пряму отримані числа. Провівши «криву знаків» визначимо знак f(x) в кожному з інтервалів (рис.1). Множина, що дає розв’язки початкової нерівності заштрихована на рис.1.
.Звідси маємо х= 0, х = -1, х = -2.Нанесемо на числову пряму отримані числа. Провівши «криву знаків» визначимо знак f(x) в кожному з інтервалів (рис.1). Множина, що дає розв’язки початкової нерівності заштрихована на рис.1.

Рис.1
Дата добавления: 2018-02-28; просмотров: 561; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 )=0.
)=0. ) у кожному проміжку, на які розбивається ОДЗ.
) у кожному проміжку, на які розбивається ОДЗ.