Розв’язування рівняння з однією змінною графічним методом
Приклад 4. Розв’язати рівняння  .
.
Розв’язування.
Дане рівняння можна подати у вигляді двох функцій у=  і
і  .
.
Зобразимо на одному малюнку графіки функцій у=  і
і  . (мал.1)
. (мал.1)
|
|

Мал.1
Точкам перетину графіків цих функцій відповідають ті значення аргументу х,при яких співпадають значення функцій, тобто корені даного рівняння.
Із малюнку видно, що рівняння має два корені, один із яких знаходиться на інтервалі (0;1), а другий – на інтервалі (2;3), а більш конкретніше х=0,2 і х=2,2
Такий метод розв’язування рівнянь називається графічним.
Графічний метод використовують якщо рівняння задано у вигляді:
f (x)=g (x).
Зображають на одному малюнку графіки функцій у= f (x) і  g (x) та знаходимо їх точки перетину.
g (x) та знаходимо їх точки перетину.  Точкам перетину графіків цих функцій відповідають ті значення аргументу х,при яких співпадають значення функцій, тобто корені даного рівняння.
Точкам перетину графіків цих функцій відповідають ті значення аргументу х,при яких співпадають значення функцій, тобто корені даного рівняння.
Графічний метод показує скільки коренів буде мати рівняння та наближено указує проміжки на числовій прямій, де ці корені можуть знаходитись.(приклад 4, мал.1).
Якщо рівняння має вид f (x)=0, то в якості функції, яка стоїть у правій частині буде у=0. Графіком її буде вісь х, тому коренями рівняння f (x)=0 будуть абсциси точок перетину графіка функції у= f (x) з віссю х.
Однорідні рівняння. Розв’язування однорідних рівнянь методом ділення кожного доданка на старший степінь.
Однорідні рівняння – це рівняння, в яких кожен з доданків має один і той же степінь. Такі рівняння розв’язуються методом ділення кожного доданка на старший степінь.
|
|
|
Приклад 5.
Розв’язати рівняння .
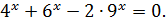 Розв’язування. Всі доданки мають один і той же степінь. Виконаємо перетворення
Розв’язування. Всі доданки мають один і той же степінь. Виконаємо перетворення
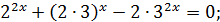
 Старший степінь 2х, то кожний доданок розділимо на
Старший степінь 2х, то кожний доданок розділимо на 
 тоді
тоді
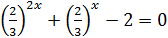 Введемо підстановку. Нехай
Введемо підстановку. Нехай 
Звідси маємо

D = 

 , тому
, тому

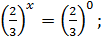 отже
отже
х = 0.
Відповідь: х=0.
Схема (алгоритм) розв’язування рівнянь з однією змінною:
1) спочатку виконаймо перетворення, використовуючи властивості та формули;
2) використаймо один із методів: розкладання на множники, підстановки (введення нової змінної величини), графічний, ділення кожного доданка на старший степінь;
3) розв’яжемо найпростіші відомі рівняння (лінійне, квадратне, степеневе, показникове, логарифмічне, тригонометричні).
Приклад 6. Розв’язати рівняння 
Розв’язування.
Необхідно позбутися від 3 у правій частині, для цього виконаємо перетворення. Подамо

 тоді початкове рівняння буде мати вид:
тоді початкове рівняння буде мати вид:



Розділимо на старший степінь 

t 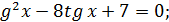 Вводимо підстановку
Вводимо підстановку
 t
t 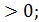

D = 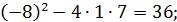


tg 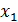 = 1;
= 1; 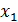 = arc tg 7 + πn, n∈ N;
= arc tg 7 + πn, n∈ N;
tg  ∈ N.
∈ N.
Відповідь: 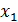 = arc tg 7 + πn, n∈ N;
= arc tg 7 + πn, n∈ N;  ∈N
∈N
ЗАПИТАННЯ І ЗАВДАННЯ ДЛЯ ПОВТОРЕННЯ
1.Яку рівність із змінною називають рівнянням?
|
|
|
2. Що означає розв’язати рівняння з однією змінною?
3. Що називається коренем рівняння з однією змінною?
4.Сформулювати основні властивості рівнянь та наслідок з них.
5.Які два рівняння називаються рівносильними?
6.Які основні види рівнянь з однією змінною ви знаєте?
7. Скільки коренів має лінійне рівняння?
8. Скільки коренів має квадратне рівняння?
9. Скільки коренів має просте степеневе рівняння при різних n і а (n- натуральне число)?
10. Скільки коренів має просте показникове рівняння при різних а і b ?
11. При яких значеннях а тригонометричні рівняння sinx=a та cosx=a не мають розв’язків
12. Які етапи (кроки) необхідно виконати, щоб розв’язати рівняння з однією змінною.
13. Назвати основні методи розв’язування рівнянь з однією змінною.
14. Як розкласти многочлен на множники способом групування?
15. Сформулюйте теорему Безу.
16.Коли застосовують метод підстановки ( введення нової змінної)?
17. В чому полягає метод розкладання на множники.
18. В чому полягає графічний метод.
ВПРАВИ
Початковий та середній рівень.
1.Які рівняння рівносильні: sinx =2; tg x = 2; 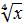 =2; 2х + 3=2;
=2; 2х + 3=2;  = -2;
= -2;
2х - 6=4; х - 2=4; 3х - 6=0; 2х=4; х2 - 9=0 х+3=0; х2 - 3х – 4=0 х+1=0.
2. Яке рівняння не має коренів:  = 0,9;
= 0,9;  = −1; х3 = −0,9;
= −1; х3 = −0,9;  = −1; sinx =2
= −1; sinx =2  = 1; х3 = 2;
= 1; х3 = 2;  = 1.
= 1.
|
|
|
3. Розв’яжіть рівняння:
1) 5х+4=0;
2) 
3) 2х2+5х-3=0;
4) х4 - 8х = 0;
5)х3 – х2 = 0;
6) 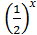 =3+х.
=3+х.
Достатній рівень
7) log32x - 4log3x+3=0;
8)  0;
0;
9) х3+3х2+5х+3=0 ;
10) cos2 x - 3sinx  cosx +1= 0;
cosx +1= 0;
11)23х−8∙22х−2х+8=0;
12) sin2x+ 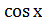 =0;
=0;
Високий рівень
13) Розв’яжіть рівняння 
14) 9  = 0;
= 0;
15) 2  = 5
= 5  ;
;
16) sinx+sin2x+sin3x = 0;
17) 6sin2 x − 3sin x cos x − 5cos2 x = 2 .
САМОСТІЙНА РОБОТА №1
Варіант -1
Розв’язати рівняння
6б 1. х2 – 2х- 8=0;
2. х3 +16х=0;
9б 3. 33х−9∙32х−3х+9=0;
4.  =2+х;
=2+х;
10-11б
5. х3+3х2 +5х+3=0.
6.6sin2 x − 3sin x cos x − 5cos2 x = 2 .
Варіант-2
Розв’язати рівняння
6б 1. х2 – 6х + 8=0;
2. х4 - 16х2 =0;
9б 3.  x+
x+  -2=0;
-2=0;
4. 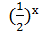 =3 - х;
=3 - х;
10-11б
5. х3+3х2 +5х+3=0.
6. 
Тема. РОЗВ’ЯЗУВАННЯ ЗАДАЧ, ЯКІ ЗВОДЯТЬСЯ ДО РІВНЯНЬ
Дата добавления: 2018-02-28; просмотров: 788; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
