Загальні методи розв’язування рівнянь з однією змінною

1) Розкладання на множники.

Якщо дане рівняння при допомозі перетворень можна звести до виду

f(x)∙g(x)=0. То дане рівняння буде рівносильне сукупності двох більш простих рівнянь в області визначення рівняння f(x)∙g(x)=0

Цей метод часто застосовується при розв’язуванні алгебраїчних рівнянь степеня вище другого, при розв’язуванні тригонометричних рівнянь.

Приклад 1. Розв’язати рівняння2cosxcos3x=cosx.

Розв’язування.

2cosxcos3x=cosx ˂=˃ 2cosxcos3x – cosx=0˂=˃ cosx(2cos3x – 1)=0˂=˃

˂=˃

Або можна розв’язок оформити так:

2cosxcos3x=cos, 2cosxcos3x – cosx=0, cosx(2cos3x – 1)=0,

Тепер задача звелася до розв’язування сукупності рівнянь cosx=0, . З рівняння cosx=0, знаходимо ,

З рівняння знаходимо cos3x= далі 3х= arccos + 2k ,

Таким чином розв’язок початкового рівняння такий: ,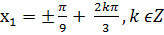

Відповідь:

Ціле раціональне рівняння. Теорема Безу.

Дане рівняння х³ - 5х² - 2х + 24=0, яке називаєтьсярівнянням степеня вище другого або рівнянням вищого степеня ми розв’язати не можемо, тому що немає знань.

Алгебра довгий час розвивалася як наука про розв’язування рівнянь і насамперед рівнянь

+a_n= 0 (n ).

Рівняння виду +a_n = 0 (n )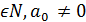

називаються алгебраїчними рівняннями степеня n.

Якщо n=1, то a₀x+a₁= 0 - лінійне рівняння.

Якщо n= 2, то a₀x² + a₁x + a₂ = 0 – квадратне рівняння.

Якщо n 2, то рівняння називається рівнянням степеня вище другого або рівнянням вищого степеня.

Алгебраїчне рівняння степеня n має не більше n дійсних коренів.

Рівняння +a_n=0 називається незведеним цілим раціональним рівнянням ( ).

Рівняння +p_n=0 називається зведеним цілим раціональним рівнянням.

Позначимо P_n(x)= +a_n. Для рівняння справедлива теорема Безу:многочлен Р_n(х) ділиться без остачі на двочлен (х - а) в тому і тільки тому випадку, коли а корінь многочлена Р_n(х).

Зауваження. Теорема Безу нерідко формується у такій спосіб: остача від ділення многочлена Р_n(х) на двочлен (х - а) дорівнює значенню цього многочлена Р_n(х) при х = а, тобто Р_n(х)=r, де r- остача від ділення многочлена Р_n(х) на двочлен (х - а).

Якщо Р_n(х) - многочлен з цілими коефіцієнтами, то всякий цілий корінь многочлена Р_n(х) є дільником вільного члена a_n.

Якщо нескоротний дріб є коренем незведеного цілого раціонального рівняння з цілими коефіцієнтами +

+a_n=0, то є дільником старшого коефіцієнта а₀, а р є дільником вільного члена a_n.

Тільки у 18 столітті була доведена основна теорема алгебри, про розв’язування рівнянь степеня n, яка була названа в честь французького математика Етьєн Безу.

Схема (алгоритм) розв’язування рівнянь вищих степенів, що мають хоча б один цілий корінь:

1) знаходять множину дільників вільного члена a_n;

2) за теоремою Безу перевіряють, які з цих дільників є розв’язком рівняння

Р_n(х)=0;

3)діленням у стовпчик знаходять частку від ділення Р_n(х) на (х-х₁), де х₁- корінь рівняння Р_n(х)=0;

4) записують частку Q_n_-1(x) як багаточлен степеня (n-1): Q_n_-1(x)

Р_n(х)= (х-х₁)∙ Q_n_-1(x), де Q_n_-1(x) многочлен степеня (n-1);

5) визначають, якщо це можливо, корені многочлена Q_n_-1(x), які також є коренями початкового рівняння.

Приклад 2. Розв’язати рівняннях³ - 5х² - 2х + 24=0.

Розв’язування. Виписуємо дільники вільного члена 24:

Підставляючи у початкове рівняння замість х=-1, дістаємо 20 0, отже х=-1 не є коренем початкового рівняння.

При х=1 маємо 18 0, отже х=1 не є коренем.

При х=-2, маємо -24+24=0, отже х=-2 є коренем початкового рівняння.

За теоремою Безу початковий многочлен без остачі ділиться на (х+2). Виконаємо ділення у стовпчик:

_х³ - 5х² - 2х + 24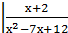

х³+2х²

-7х² - 2х

-7х² - 14х

12х + 24

Таким чином х³ - 5х² - 2х + 24=(х+2)( х² - 7х + 12), отже початкове рівняння набуває вигляду (х+2)( х² - 7х + 12)=0. Це рівняння рівносильне сукупності рівнянь х+2=0 і х² - 7х + 12=0 . Розв’язок першого з яких уже знайдено х= -2. Розв’язуємо друге рівняння х² - 7х + 12=0, яке має корені х=3 і х=4. Отже початкове рівняння має три корені: х₁=-2, х₂=3, х₃=4.

Відповідь:

2) Розв’язування рівняння з однією змінною методом підстановки.

Якщо в рівнянні є одинакові вирази зі змінною величиною, які можна замінити новою змінною величиною, то отримаємо більш прості рівняння.

Приклад3. Розв’язати рівняння(х²+3х)² +2(х²+3х) -120=0.

Розв’язування.

Якщо х²+3х= у, то отримали зведене квадратне рівняння у² +2у -120=0; звідси у₁= -12 і у₂= 10, тому отримали два рівняння х²+3х=-12 і х²+3х=10. Розв’яжемо їх кожне окремо відносно х. Розв’яжемо перше з них

х²+3х=-12, х²+ 3х +12=0,

Розв’яжемо друге з них х²+ 3х – 10 = 0, D=49, = ;

= -2 і = 5. Отже рівняння (х²+3х)² +2(х²+3х) -120=0 має два корені

= -2 і = 5.

Відповідь: -2; 5.

Дата добавления: 2018-02-28; просмотров: 563; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!